Смята се, че концепцията за числата възниква за първи път, когато праисторическите хора са започнали да използват пръстите си, за да броят нещо. Оттогава човечеството е изминало дълъг път. Сега използваме калкулатори и компютри, за да броим най-големите числа. И дори имена са се появили за числа, които са толкова големи, че едва ли могат да бъдат представени.
Безкрайност на преброими числа
Изглежда, че отговорът на въпроса кой е най-големият брой в математиката е много прост. Безкрайност, нали? Но това не е съвсем правилно. В крайна сметка безкрайността изобщо не е число, а концепция. Идея.
Безкрайността (infinitum) е понятие, което в превод от латински означава „без граници“. Определението за безкрайност в математиката казва, че колкото и голямо да е число, винаги можете да добавите 1 към него и то ще стане по-голямо.
Следователно, строго погледнато, няма такова нещо като най-големия брой в света. Можете да назовете само най-големия номер с конкретно име.
Някои от най-известните имена за голям брой са:
| Брой нули | Име | Име на английски |
|---|---|---|
| 3 | хиляди | хиляди |
| 6 | милиона | милиона |
| 9 | милиард (милиард) | милиард |
| 12 | трилион | трилион |
| 15 | квадрилион | квадрилион |
| 18 | квинтилион | квинтилион |
| 21 | секстилион | секстилион |
| 24 | септилион | септилион |
| 27 | октилион | октилион |
| 30 | квинтилион | нонилион |
| 33 | децилион | децилион |
| 36 | недецилион | недецилион |
| 39 | дуодецилион | дуодецилион |
| 42 | тредецилион | тредецилион |
| 45 | квадуорддецилион | четвъртидецилион |
| 48 | квиндецилион | квиндецилион |
| 51 | sexdecillion | sexdecillion |
| 54 | септендецилион | септендецилион |
| 57 | октодецилион | октодецилион |
| 60 | ноемвридецилион | ноемвридецилион |
| 63 | вигинтилион | вигинтилион |
| 66 | неподходящо | неподходящо |
| 69 | дуовигинтилион | дуовигинтилион |
| 72 | тревигинтилион | тревигинтилион |
| 75 | quatuorvigintillion | quattuorvigintillion |
| 78 | квинвигинтилион | квинвигинтилион |
| 81 | sexvigintillion | sexvigintillion |
| 84 | septenvigintillion | septenvigintillion |
| 87 | октовигинтилион | октовигинтилион |
| 90 | novemvigintillion | novemvigintillion |
| 93 | тригинтилион | тригинтилион |
| 96 | неприсъединителен | неприсъединителен |
| 99 | дуотригинтилион | дуотригинтилион |
| 102 | третигрилин | трестригинтилион |
| 105 | кватригинтилион | quattuortrigintillion |
| 108 | квинтригинтилион | квинтригинтилион |
| 111 | секстригинтилион | секстригинтилион |
| 114 | септентригинтилион | септентригинтилион |
| 117 | октотригинтилион | октотригинтилион |
| 120 | novemtrigintillion | novemtrigintillion |
| 123 | квадрагинтилион | квадрагинтилион |
| 126 | неквадрагинтилион | неквадрагинтилион |
| 129 | duoquadragintillion | duoquadragintillion |
| 132 | trackquadragintillion | треквадрагинтилион |
| 135 | quatorquadragintillion | quattuorquadragintillion |
| 138 | quinquadragintillion | quinquadragintillion |
| 141 | sexquadragintillion | sexquadragintillion |
| 144 | септинкуадрагинтилион | septenquadragintillion |
| 147 | октоквадрагинтилион | октоквадрагинтилион |
| 150 | novemquadragintillion | novemquadragintillion |
| 153 | квинквагинтилион | квинквагинтилион |
| 156 | unquincagintillion | неквинквагинтилион |
| 159 | duoquincagintillion | duoquinquagintillion |
| 162 | trequincagintillion | trequinquagintillion |
| 165 | quatorquincagintillion | quattuorquinquagintillion |
| 168 | quinquincagintillion | quinquinquagintillion |
| 171 | sexquincagintillion | sexquinquagintillion |
| 174 | septenquincagintillion | septenquinquagintillion |
| 177 | октокинкагинатилион | октохинкуагинтилион |
| 180 | novemquincagintillion | novemquinquagintillion |
| 183 | сексагинтилион | сексагинтилион |
| 186 | несексагинтилион | несексагинтилион |
| 189 | дуосексагинтилион | дуосексагинтилион |
| 192 | тресексагинтилион | тресексагинтилион |
| 195 | кваторсексагинтилион | quattuorsexagintillion |
| 198 | хинсексагинтилион | хинсексагинтилион |
| 201 | sexsexagintillion | sexsexagintillion |
| 204 | septensexagintillion | septensexagintillion |
| 207 | октосексагинтилион | октосексагинтилион |
| 210 | novemsexagintillion | novemsexagintillion |
| 213 | септагинтилион | септуагинтилион |
| 216 | несептагинтилион | unseptuagintillion |
| 219 | дуосептагинтилион | дуосептуагинтилион |
| 222 | тресептагинтилион | treseptuagintillion |
| 225 | кваторсептагинтилион | quattuorseptuagintillion |
| 228 | квинсептагинтилион | quinseptuagintillion |
| 231 | sexseptagintillion | sexseptuagintillion |
| 234 | септенсептагинтилион | septenseptuagintillion |
| 237 | октозептагинтилион | октосептуагинтилион |
| 240 | novemseptagintillion | novemseptuagintillion |
| 243 | октогинтилион | октогинтилион |
| 246 | уноктогинтилион | уноктогинтилион |
| 249 | дуоктоктогинтилион | дуоктоктогинтилион |
| 252 | tracktogintillion | треоктогинтилион |
| 255 | кватороктогинтилион | quattuoroctogintillion |
| 258 | хиноктогинтилион | хиноктогинтилион |
| 261 | sexoctogintillion | сексоктогинтилион |
| 264 | septoktogintillion | септоктогинтилион |
| 267 | октоктогинтилион | октооктогинтилион |
| 270 | новемоктогинтилион | новемоктогинтилион |
| 273 | нонагинтилион | нонагинтилион |
| 276 | ненадминат | ненадминат |
| 279 | дуононагинтилион | дуононагинтилион |
| 282 | тренонагинтилион | тренонагинтилион |
| 285 | quatornonagintillion | quattuornonagintillion |
| 288 | хинонагинтилион | хинонагинтилион |
| 291 | sexnagintillion | sexnonagintillion |
| 294 | septennonagintillion | septennonagintillion |
| 297 | октононагинтилион | октононагинтилион |
| 300 | novemnonagintillion | novemnonagintillion |
| 303 | центилион | центилион |
Как се нарича най-голямото просто число
 Прост брой е този, който се дели само от себе си и от един. В края на 2018 г. американецът Патрик Ларош представи най-голямото просто число на научния свят.
Прост брой е този, който се дели само от себе си и от един. В края на 2018 г. американецът Патрик Ларош представи най-голямото просто число на научния свят.
- Дължината му е 24 862 048 знака. За сравнение: в епохалното произведение на Л.Н. „Война и мир“ на Толстой е около 6-7 милиона знака, ако включите пунктуация и интервали.
- Това число може да бъде записано по следния начин: 282589933-1
- И се чете така: две в степен 82589933 минус едно.
- Има цял онлайн проект GIMPS, насочен точно към намирането на най-големите прости числа. В него участват математици от различни страни. Следователно новите носители на записи се появяват често. Учените работят, както се казва, не от страх, а заради пари. В крайна сметка, който отвори следващия най-голям Mersenne prime, ще получи 3000 долара.
Кой е най-големият брой в света
 През 1980 г. в Книгата на рекордите на Гинес е включен номерът на Греъм (известен също като G64 или G), кръстен на американския математик Роналд Греъм. Това е най-големият брой, използван някога във важно математическо доказателство. Говорим за теорията на Франк Рамзи.
През 1980 г. в Книгата на рекордите на Гинес е включен номерът на Греъм (известен също като G64 или G), кръстен на американския математик Роналд Греъм. Това е най-големият брой, използван някога във важно математическо доказателство. Говорим за теорията на Франк Рамзи.
Накратко за тази теория: представете си N-измерен куб, върховете му са произволно свързани чрез червени или сини сегменти на линията. И нашата задача е да разберем до каква стойност на N е възможно (ако ръбовете на куба са боядисани по различни начини), за да избегнем ситуация, при която една равнина в куба ще бъде боядисана с един цвят. Тоест не бива да получаваме едноцветен „плик“.
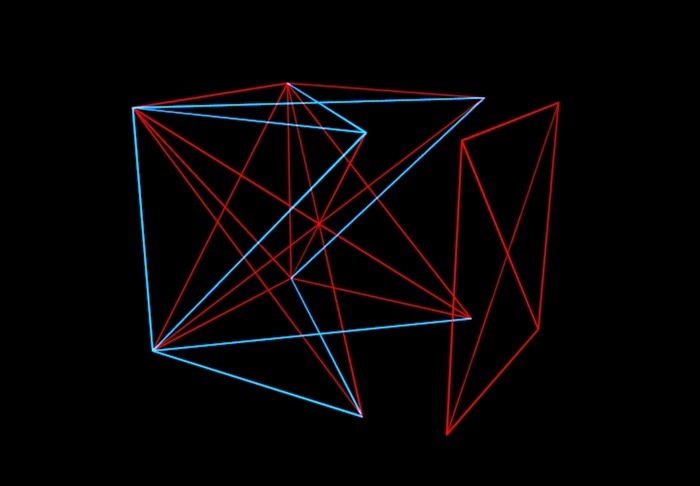
Математиците нарисуваха куба по този начин и така, оказа се, че до шестизмерен куб можете да измислите и да направите линиите от един и същи цвят, свързващи четирите върха, да не лежат в една и съща равнина. Но със седемизмерното, както откриха Греъм и Ротшилд, подобен трик вече не е възможен. И с осеммерна. И ... „и така нататък“, което обаче не е безкрайно, а завършва с фантастично гигантско число. Това наричат номера на Греъм. Между другото, решението на Греъм и Ротшилд вече е остаряло. Математиците са открили, че 6-7-8-9-10-11-12-12-мерните кубчета все още могат да бъдат боядисани без „пликове“. Но някъде между 13 и числото на Греъм, гарантирано ще има число, над което във всеки случай ще има "пликове".
Номерът на Греъм получи световно признание през 1977 г., когато известният популяризатор на науката Мартин Гарднър пише за това в Scientific American.
И въпреки че оттогава има и други кандидати за титлата с най-голям брой по математика, „въображението“ на Греъм е най-популярното и добре познато. И ако сте чували за „семейството на въглищата“:
- googol - 10100;
Или: 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 - googolplex - 10googol,
тогава трябва да знаете, че тези числа в математиката са просто "месене", а числото на Греъм е немислим брой пъти по-голямо от тях. И дори повече от Skuse число между 1019 и 1.3971672 10316 и приблизително равни д727,951336108.
Любопитното е, че чрез изобретяването на googol американският математик Едуард Казнер искаше да покаже на учениците разликата между невероятно голям брой и безкрайност. Тогава номерът на Греъм може просто „да ви взриви ума“.
Възможно ли е да си представим и запишем число, което е неразбираемо
Математиците няма да могат да ви кажат точния брой цифри в броя на Греъм, да не говорим за него. Известни са само последните 50 цифри от най-големия брой в света - това е ... 03222348723967018485186439059104575627262464195387.
Но номерата, с които започва G64, са неизвестни и е малко вероятно някога да бъдат.
Нека сравним три чудовища: googol, googolplex и числото на Греъм.
- Googol е броят на зърната пясък, които могат да се поберат във Вселената, умножен по 10 милиарда.И така, представете си вселена, изпълнена с малки пясъчни зърна - десетки милиарди светлинни години над Земята, под нея, пред нея, зад нея - безкраен пясък.
Сега си представете, че в даден момент вземете едно зрънце пясък, за да го изследвате под мощен микроскоп. И виждате, че всъщност това не е единственото зърно, а 10 милиарда микроскопични зърна и заедно те са с размерите на зърно пясък. Ако случаят беше такъв за всяко отделно зърно пясък в тази хипотетична вселена, тогава общата сума на тези микроскопични зърна би била гугол.
- За количествено определяне на googolplex, астрономът и астрофизик Карл Сейгън даде пример за пълнене на целия обем на наблюдаваната Вселена с фини прахови частици с размер приблизително 1,5 микрометра. Въз основа на това общият брой на различни комбинации, в които тези частици могат да бъдат разположени, ще бъде приблизително равен на един googolplex.
- А сега си представете, че googolplex не е дори песъчинка, а малка точка, която може да се види само чрез най-мощния микроскоп. И цялата ни Вселена е изпълнена с такива малки точки. Така че, дори това не се сравнява с броя на Греъм. Но какво, ако искаме да използваме цялото пространство на наблюдаваната вселена, за да го запишем (да предположим, че записването на всяка цифра заема поне обема на Планк)? Уви, това няма да работи за нас! Но винаги можете да отидете по друг път.
Как да напиша G64, използвайки метода на Кнут
През 1976 г. американският учен Доналд Кнут предлага концепцията за суперстепените или нотацията на Кнут. Това е метод, който ви позволява да пишете много големи числа, използвайки стрелките нагоре. Степенуването се обозначава с една стрелка нагоре: ↑.
Ето как изглежда тази нотация: a ↑ b = ab = a × a × a × ... и т.н. b пъти.
- Например 3 ↑ 3 = 3³.
- Googol е написан като 10 ↑ 10 ↑ 2.
- Гугълплекс - 10 ↑ 10 ↑ 10 ↑ 2
Важна характеристика на стрелките нагоре е, че те растат много бързо. Експозицията расте много по-бързо от умножението. 2 × 10 е само 20, но 2 ↑ 10 = 1024. По същия начин всяко ново ниво на стрелките расте много по-бързо от предишното ниво.
Ако си представите мислено силова кула от тризнаци 3 ↑↑↑ 4, ще получите структура с размери от Земята до Марс. Но дори не сме достигнали „долната стъпало“, което ни води до числото на Греъм.
Можем да опишем числото на Греъм с огромен набор от тези стрелки нагоре.
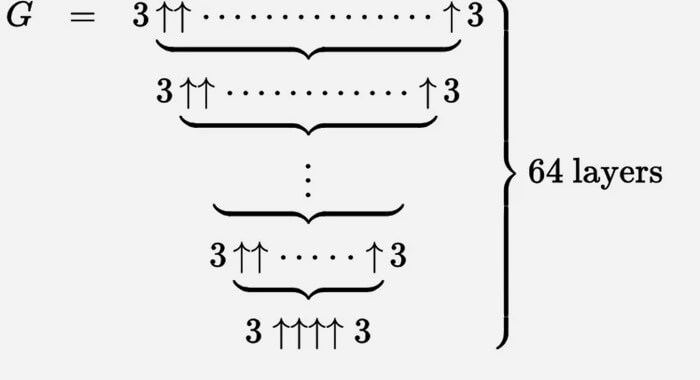
Най-лесно е да мислим за това като за итеративен процес. Започваме отдолу с g 1 = 3 ↑↑↑↑ 3 и след това създаваме втори ред (да го наречем g 2) със g 1 стрелки между тризнаците.
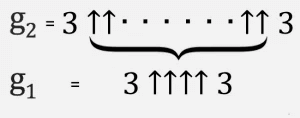
Тогава g 3 е две тройки, разделени от g 2 със стрелки нагоре и така нататък, докато g 64 със стрелки g 63 между тройките е число на Греъм.
Ако изберете безжитие, равно на числото на Греъм, резултатът ще бъде почти същият. Дори да приемем, че условията във Вселената, в Слънчевата система и на Земята ще останат завинаги непроменени, човешкият мозък не би могъл да издържи толкова дълъг период от време без вредни промени.

