Sayı kavramının ilk olarak tarih öncesi insanların parmaklarını bir şeyler saymak için kullanmaya başladıklarında ortaya çıktığına inanılıyor. O zamandan beri insanlık uzun bir yol kat etti. Artık en büyük sayıları saymak için hesap makineleri ve bilgisayarları kullanıyoruz. Ve hayal bile edilemeyecek kadar büyük sayılar için isimler bile ortaya çıktı.
Sayılabilir sayıların sonsuzluğu
Matematikte en büyük sayının ne olduğu sorusunun cevabı çok basit görünüyor. Infinity, değil mi? Ancak bu tamamen doğru değil. Sonuçta sonsuzluk bir sayı değil, bir kavramdır. Fikir.
Sonsuzluk (infinitum), Latince'den çevrildiğinde "sınırsız" anlamına gelen bir kavramdır. Matematikte sonsuzluğun tanımı, bir sayı ne kadar büyük olursa olsun, ona her zaman 1 ekleyebileceğinizi ve daha da büyüyeceğini söylüyor.
Bu nedenle, kesinlikle konuşursak, dünyadaki en büyük sayı diye bir şey yoktur. Yalnızca belirli bir ad verilen en büyük numarayı adlandırabilirsiniz.
Büyük sayılar için daha ünlü isimlerden bazıları:
| Sıfır sayısı | İsim | İngilizce isim |
|---|---|---|
| 3 | bin | bin |
| 6 | milyon | milyon |
| 9 | milyar (milyar) | milyar |
| 12 | trilyon | trilyon |
| 15 | katrilyon | katrilyon |
| 18 | kentilyon | kentilyon |
| 21 | seksilyon | seksilyon |
| 24 | septilyon | septilyon |
| 27 | sekiz milyon | sekiz milyon |
| 30 | kentilyon | nonilyon |
| 33 | desilyon | desilyon |
| 36 | undesilyon | undesilyon |
| 39 | duodecillion | duodecillion |
| 42 | tredecillion | tredecillion |
| 45 | kuatuorddecillion | Quattuordecillion |
| 48 | beş milyar | beş milyar |
| 51 | seksdecillion | seksdecillion |
| 54 | septendecillion | septendecillion |
| 57 | sekizdesimilyon | sekizdesimilyon |
| 60 | Novemdecillion | Novemdecillion |
| 63 | vigintillion | vigintillion |
| 66 | vigintilyon | vigintilyon |
| 69 | duovigintillion | duovigintillion |
| 72 | Trevigintillion | Trevigintillion |
| 75 | kuatuorvigintillion | Quattuorvigintillion |
| 78 | beşinci milyon | beşinci milyon |
| 81 | sexvigintillion | sexvigintillion |
| 84 | Septenvigintillion | Septenvigintillion |
| 87 | oktovigintilyon | oktovigintilyon |
| 90 | Novemvigintillion | Novemvigintillion |
| 93 | trigintillion | trigintillion |
| 96 | trigintilyon | trigintilyon |
| 99 | duotrigintillion | duotrigintillion |
| 102 | Tretrigintillion | Trestrigintillion |
| 105 | Quattrigintillion | Quattuortrigintillion |
| 108 | beşte birlik dilim | beşte birlik dilim |
| 111 | sekstrigintilyon | sekstrigintilyon |
| 114 | septentrigintillion | septentrigintillion |
| 117 | oktotrigintilyon | oktotrigintilyon |
| 120 | Novemtrigintillion | Novemtrigintillion |
| 123 | katragintilyon | katragintilyon |
| 126 | Unquadragintillion | Unquadragintillion |
| 129 | duoquadragintillion | duoquadragintillion |
| 132 | Trackquadragintillion | Trequadragintillion |
| 135 | Quatorquadragintillion | Quattuorquadragintillion |
| 138 | beş yüzlük | beş yüzlük |
| 141 | sexquadragintillion | sexquadragintillion |
| 144 | Septinquadragintillion | Septenquadragintillion |
| 147 | Octoquadragintillion | Octoquadragintillion |
| 150 | Novemquadragintillion | Novemquadragintillion |
| 153 | beş milyon | beş milyon |
| 156 | eşit olmayan | Unquinquagintillion |
| 159 | duoquincagintillion | duoquinquagintillion |
| 162 | Trequincagintillion | Trequinquagintillion |
| 165 | Quatorquincagintillion | Quattuorquinquagintillion |
| 168 | beşinci milyon | Quinquinquagintillion |
| 171 | seksquincagintillion | seksquinquagintillion |
| 174 | Septenquincagintillion | Septenquinquagintillion |
| 177 | sekiz-sekizlik | oktokinquagintillion |
| 180 | Novemquincagintillion | Novemquinquagintillion |
| 183 | sexagintillion | sexagintillion |
| 186 | Unsexagintillion | Unsexagintillion |
| 189 | duosexagintillion | duosexagintillion |
| 192 | treseksagintilyon | treseksagintilyon |
| 195 | Quatorsexagintillion | quattuorsexagintillion |
| 198 | beş yüz seksilyon | beş yüz seksilyon |
| 201 | seksiseksagintillion | seksiseksagintillion |
| 204 | Septensexagintillion | Septensexagintillion |
| 207 | sekizlik seks | sekizlik seks |
| 210 | Novemsexagintillion | Novemsexagintillion |
| 213 | septagintillion | septuagintillion |
| 216 | septagintillion | unseptuagintillion |
| 219 | duoseptagintillion | duoseptuagintillion |
| 222 | Treseptagintillion | Treseptuagintillion |
| 225 | Quatorseptagintillion | Quattuorseptuagintillion |
| 228 | Quinseptagintillion | Quinseptuagintillion |
| 231 | Sexseptagintillion | Sexseptuagintillion |
| 234 | septenseptagintillion | septenseptuagintillion |
| 237 | Octoseptagintillion | Octoseptuagintillion |
| 240 | Novemseptagintillion | Novemseptuagintillion |
| 243 | oktogintilyon | oktogintilyon |
| 246 | oktogintilyon | oktogintilyon |
| 249 | duooctogintillion | duooctogintillion |
| 252 | Tracktogintillion | Treoctogintillion |
| 255 | Quatoroktogintillion | Quattuoroctogintillion |
| 258 | kinoktogintilyon | beştogintilyon |
| 261 | seksoktogintilyon | seksoktogintilyon |
| 264 | Septoktogintillion | septoctogintillion |
| 267 | oktoktogintilyon | oktooktogintilyon |
| 270 | Novemoctogintillion | Novemoctogintillion |
| 273 | agintilyon olmayan | nonagintillion |
| 276 | parlamayan | parlamayan |
| 279 | duononagintillion | duononagintillion |
| 282 | Trenonagintillion | Trenonagintillion |
| 285 | Quatornonagintillion | Quattuornonagintillion |
| 288 | quinnonagintillion | quinnonagintillion |
| 291 | sexnagintillion | sexnonagintillion |
| 294 | Septennonagintillion | Septennonagintillion |
| 297 | oktononagintilyon | oktononagintilyon |
| 300 | Novemnonagintillion | Novemnonagintillion |
| 303 | Centillion | Centillion |
En büyük asal sayının adı nedir
 Bir asal sayı, yalnızca kendisine ve bire bölünebilen sayıdır. 2018'in sonunda Amerikalı Patrick Laroche, bilim dünyasına en büyük asal sayıyı sundu.
Bir asal sayı, yalnızca kendisine ve bire bölünebilen sayıdır. 2018'in sonunda Amerikalı Patrick Laroche, bilim dünyasına en büyük asal sayıyı sundu.
- Uzunluğu 24.862.048 karakterdir. Karşılaştırma için: L.N.'nin çığır açan çalışmasında. Noktalama işaretleri ve boşluklar eklerseniz, Tolstoy'un "Savaş ve Barış" ı yaklaşık 6-7 milyon karakterdir.
- Bu numara şu şekilde yazılabilir: 282589933-1
- Ve şöyle okur: 82589933'ün üssü iki eksi bir.
- Tam olarak en büyük astarları bulmayı amaçlayan bütün bir çevrimiçi GIMPS projesi var. Farklı ülkelerden matematikçiler buna katılıyor. Bu nedenle, yeni rekor sahipleri sık sık karşımıza çıkmaktadır. Bilim adamları dedikleri gibi korku için değil, para için çalışırlar. Sonuçta, bir sonraki en büyük Mersenne prime'ı açan kişi 3.000 $ alacak.
Dünyadaki en büyük sayı nedir
 1980'de Guinness Rekorlar Kitabı, Amerikalı matematikçi Ronald Graham'ın adını taşıyan Graham numarasını (G64 veya G olarak da bilinir) içeriyordu. Önemli bir matematiksel kanıtta şimdiye kadar kullanılan en büyük sayıdır. Frank Ramsey'in teorisinden bahsediyoruz.
1980'de Guinness Rekorlar Kitabı, Amerikalı matematikçi Ronald Graham'ın adını taşıyan Graham numarasını (G64 veya G olarak da bilinir) içeriyordu. Önemli bir matematiksel kanıtta şimdiye kadar kullanılan en büyük sayıdır. Frank Ramsey'in teorisinden bahsediyoruz.
Bu teori hakkında kısaca: N boyutlu bir küp hayal edin, köşeleri rastgele kırmızı veya mavi çizgi parçalarıyla birbirine bağlanır. Ve bizim görevimiz, küpteki bir düzlemin tek renkle boyanacağı bir durumdan kaçınmanın mümkün olduğunu anlamaktır (eğer küpün kenarları farklı şekillerde boyanmışsa). Yani tek renkli bir "zarf" almamalıyız.
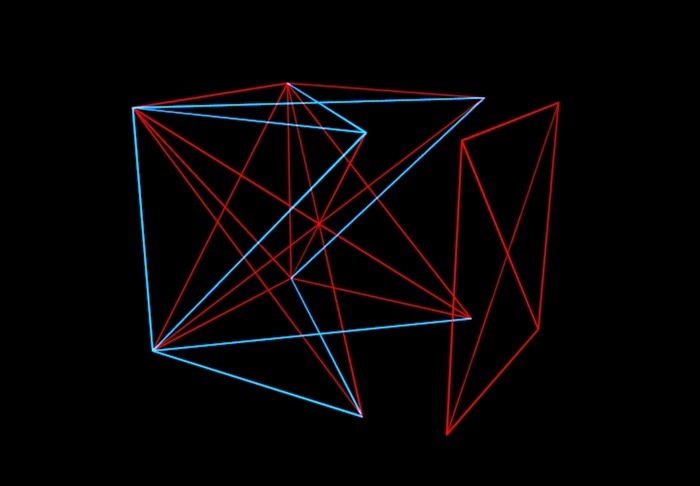
Matematikçiler küpü bu şekilde boyadılar ve bu, altı boyutlu bir kübe kadar, dört köşeyi birbirine bağlayan aynı renkteki çizgilerin aynı düzlemde uzanmamasını sağlayabileceğiniz ve yapabileceğiniz ortaya çıktı. Ancak Graham ve Rothschild'in de keşfettiği gibi yedi boyutlu ile böyle bir numara artık mümkün değil. Ve sekiz boyutlu. Ve ... "ve benzeri", ancak sonsuz değildir, ancak fevkalade devasa bir sayı ile biter. Graham'ın numarası dedikleri bu. Bu arada, Graham ve Rothschild'in çözümü artık modası geçmiş durumda. Matematikçiler 6-7-8-9-10-11-12 boyutlu küplerin hala zarfsız boyanabileceğini keşfettiler. Ancak 13 ile Graham'ın numarası arasında bir yerde, her durumda "zarfların" olacağı bir sayı olması garanti edilir.
Graham'ın sayısı, 1977'de ünlü bilim popülerleştiricisi Martin Gardner'ın Scientific American'da yazmasıyla dünya çapında tanındı.
Ve o zamandan beri matematikteki en büyük sayı unvanı için başka adaylar olmasına rağmen, Graham'ın "beyin çocuğu" en popüler ve tanınmış olanıdır. Ve "kömür ailesi" ni duyduysanız:
- googol - 10100;
Veya: 100000000000 000000000000000000 000000000000000000000000 000000 000000000000000000 000000 000000000 000000000 - googolplex - 10googol,
o zaman matematikteki bu sayıların sadece "yoğurucu" olduğunu ve Graham'ın sayısının onlardan çok daha büyük bir sayı olduğunu bilmelisiniz. Ve 10 arasında bir Skuse sayısından bile fazlası19 ve 1.3971672 10316 ve yaklaşık olarak eşit e727,951336108.
Merakla, Amerikalı matematikçi Edward Kazner googol'u icat ederek, öğrencilere inanılmaz derecede büyük sayı ile sonsuzluk arasındaki farkı göstermek istedi. O zaman Graham'ın numarası "aklınızı başınızdan alabilir" olabilir.
Anlamanın ötesinde bir sayı hayal etmek ve yazmak mümkün mü
Matematikçiler, Graham'ın sayısındaki tam rakamları size söyleyemezler, onu saymayı bırakın. Dünyadaki en büyük sayının yalnızca son 50 hanesi bilinmektedir - bu ... 03222348723967018485186439059104575627262464195387.
Ancak G64'ün başladığı sayılar bilinmemektedir ve hiçbir zaman olması muhtemel değildir.
Üç canavarı karşılaştıralım: googol, googolplex ve Graham'ın numarası.
- Googol, evrene sığabilecek kum tanesi sayısının 10 milyar ile çarpımıdır.Öyleyse, küçük kum taneleri ile dolu bir evren hayal edin - Dünyanın on milyarlarca ışık yılı yukarısında, altında, önünde, arkasında - sonsuz kum.
Şimdi bir noktada güçlü bir mikroskop altında incelemek için bir kum tanesi aldığınızı hayal edin. Ve görüyorsunuz ki bu aslında tek bir tane değil, 10 milyar mikroskobik tanecik ve hepsi birlikte bir kum tanesi büyüklüğünde. Bu varsayımsal evrendeki her bir kum tanesi için durum böyle olsaydı, bu mikroskobik tanelerin toplamı bir googol olurdu.
- Googolplex'i ölçmek için astronom ve astrofizikçi Carl Sagan, gözlemlenebilir evrenin tüm hacmini yaklaşık 1.5 mikrometre boyutunda ince toz parçacıklarıyla doldurmanın bir örneğini verdi. Buna dayanarak, bu parçacıkların yerleştirilebileceği farklı kombinasyonların toplam sayısı yaklaşık olarak bir googolplex'e eşit olacaktır.
- Şimdi bir googolplex'in bir kum tanesi bile olmadığını, ancak en güçlü mikroskopla görülebilen küçük bir nokta olduğunu hayal edelim. Ve tüm evrenimiz çok küçük noktalarla dolu. Yani, bu bile Graham'ın sayısıyla karşılaştırılamaz. Peki ya gözlemlenebilir evrenin tüm uzayını onu kaydetmek için kullanmak istiyorsak (her basamağın kaydedilmesinin en azından Planck hacmini kapladığını varsayalım)? Ne yazık ki, bu bizim için işe yaramayacak! Ama her zaman diğer tarafa gidebilirsin.
Knuth yöntemini kullanarak G64 nasıl yazılır
1976'da Amerikalı bilim adamı Donald Knuth, süper derece kavramını veya Knuth'un gösterimini önerdi. Bu, yukarı doğru işaret eden okları kullanarak çok büyük sayılar yazmanıza izin veren bir yöntemdir. Üs alma, bir yukarı okla gösterilir: ↑.
Bu gösterim şuna benziyor: a ↑ b = ab = a × a × a ×… ve böylece b kez.
- Örneğin 3 ↑ 3 = 3³.
- Googol, 10 ↑ 10 ↑ 2 olarak yazılır.
- Bir googolplex - 10 ↑ 10 ↑ 10 ↑ 2
Yukarı okların önemli bir özelliği, çok hızlı büyümeleridir. Maruz kalma, çarpmadan çok daha hızlı büyür. 2 × 10 yalnızca 20'dir, ancak 2 ↑ 10 = 1024. Aynı şekilde, her yeni ok seviyesi önceki seviyeden çok daha hızlı büyür.
Zihinsel olarak 3 ↑↑↑ 4 üçlü bir güç kulesi hayal ederseniz, boyutları Dünya'dan Mars'a kadar değişen bir yapı elde edersiniz. Ama bizi Graham'ın sayısına götüren “alt basamağa” bile ulaşmadık.
Graham'ın numarasını bu yukarı doğru okların büyük bir setiyle tanımlayabiliriz.
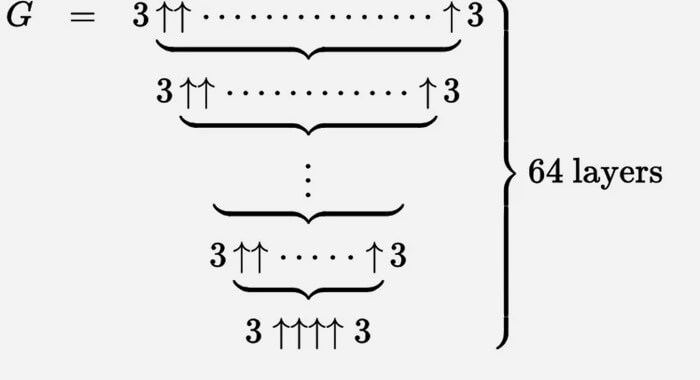
Bunu yinelemeli bir süreç olarak düşünmek en kolayıdır. En alttan g 1 = 3 ↑↑↑↑ 3 ile başlıyoruz ve sonra üçlüler arasında g 1 okla ikinci bir sıra oluşturuyoruz (g 2 diyelim).
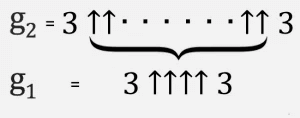
Daha sonra g 3, yukarı oklarla g2 ile ayrılan iki üçlüdür ve bu şekilde, üçlüler arasında g 63 oklu g 64, Graham sayısı olana kadar.
Ölümsüzlük yerine Graham sayısına eşit bir yaşam süresi seçerseniz, sonuç hemen hemen aynı olacaktır. Evrendeki, Güneş Sistemindeki ve Dünyadaki koşulların sonsuza kadar değişmeyeceğini varsaysak bile, insan beyninin zararlı değişiklikler olmadan bu kadar uzun bir süreye dayanması mümkün olamazdı.

