Pinaniniwalaan na ang konsepto ng mga numero ay nagmula noong nagsimula ang mga taong sinaunang-panahon na gamitin ang kanilang mga daliri upang mabilang ang isang bagay. Mula noon, malayo na ang narating ng sangkatauhan. Gumagamit kami ngayon ng mga calculator at computer upang mabilang ang pinakamalaking bilang. At kahit na ang mga pangalan ay lumitaw para sa mga bilang na napakalaki na halos hindi nila maisip.
Walang katapusan ng bilang na mabibilang
Tila ang sagot sa tanong na kung ano ang pinakamalaking bilang sa matematika ay napaka-simple. Infinity, di ba? Ngunit hindi ito ganap na tama. Pagkatapos ng lahat, ang infinity ay hindi isang numero sa lahat, ngunit isang konsepto. Idea.
Ang Infinity (infinitum) ay isang konsepto na sa pagsasalin mula sa Latin ay nangangahulugang "walang hangganan". Sinasabi ng kahulugan ng kawalang-hanggan sa matematika na gaano man kalaki ang isang numero, maaari mong palaging magdagdag ng 1 dito at ito ay magiging mas malaki.
Samakatuwid, mahigpit na nagsasalita, walang bagay tulad ng pinakamalaking bilang sa mundo. Maaari mo lamang pangalanan ang pinakamalaking bilang na binigyan ng isang tukoy na pangalan.
Ang ilan sa mga mas tanyag na pangalan para sa malaking bilang ay:
| Bilang ng mga zero | Pangalan | Pangalan sa English |
|---|---|---|
| 3 | libo | libo |
| 6 | milyon | milyon |
| 9 | bilyon (bilyon) | bilyon |
| 12 | trilyon | trilyon |
| 15 | quadrillion | quadrillion |
| 18 | quintillion | quintillion |
| 21 | sextillion | sextillion |
| 24 | septilyon | septilyon |
| 27 | milyun-milyon | milyun-milyon |
| 30 | quintillion | nonillion |
| 33 | bilyun-bilyon | bilyun-bilyon |
| 36 | undecillion | undecillion |
| 39 | duodecillion | duodecillion |
| 42 | tredecillion | tredecillion |
| 45 | quatuorddecillion | quattuordecillion |
| 48 | quindecillion | quindecillion |
| 51 | sexdecillion | sexdecillion |
| 54 | septendecillion | septendecillion |
| 57 | octodecillion | octodecillion |
| 60 | novemdecillion | novemdecillion |
| 63 | vigintillion | vigintillion |
| 66 | unvigintillion | unvigintillion |
| 69 | duovigintillion | duovigintillion |
| 72 | trevigintillion | trevigintillion |
| 75 | quatuorvigintillion | quattuorvigintillion |
| 78 | quinvigintillion | quinvigintillion |
| 81 | sexvigintillion | sexvigintillion |
| 84 | septenvigintillion | septenvigintillion |
| 87 | octovigintillion | octovigintillion |
| 90 | novemvigintillion | novemvigintillion |
| 93 | trigintillion | trigintillion |
| 96 | untrigintillion | untrigintillion |
| 99 | duotrigintillion | duotrigintillion |
| 102 | tretrigintillion | trestrigintillion |
| 105 | quattrigintillion | quattuortrigintillion |
| 108 | quintrigintillion | quintrigintillion |
| 111 | sextrigintillion | sextrigintillion |
| 114 | septentrigintillion | septentrigintillion |
| 117 | octotrigintillion | octotrigintillion |
| 120 | novemtrigintillion | novemtrigintillion |
| 123 | quadragintillion | quadragintillion |
| 126 | unquadragintillion | unquadragintillion |
| 129 | duoquadragintillion | duoquadragintillion |
| 132 | trackquadragintillion | trequadragintillion |
| 135 | quatorquadragintillion | quattuorquadragintillion |
| 138 | quinquadragintillion | quinquadragintillion |
| 141 | sexquadragintillion | sexquadragintillion |
| 144 | septinquadragintillion | septenquadragintillion |
| 147 | octoquadragintillion | octoquadragintillion |
| 150 | novemquadragintillion | novemquadragintillion |
| 153 | quinquagintillion | quinquagintillion |
| 156 | unquincagintillion | unquinquagintillion |
| 159 | duoquincagintillion | duoquinquagintillion |
| 162 | trequincagintillion | trequinquagintillion |
| 165 | quatorquincagintillion | quattuorquinquagintillion |
| 168 | quinquincagintillion | quinquinquagintillion |
| 171 | sexquincagintillion | sexquinquagintillion |
| 174 | septenquincagintillion | septenquinquagintillion |
| 177 | octoquincagintillion | octoquinquagintillion |
| 180 | novemquincagintillion | novemquinquagintillion |
| 183 | sexagintillion | sexagintillion |
| 186 | unsexagintillion | unsexagintillion |
| 189 | duosexagintillion | duosexagintillion |
| 192 | tresexagintillion | tresexagintillion |
| 195 | quatorsexagintillion | quattuorsexagintillion |
| 198 | quinsexagintillion | quinsexagintillion |
| 201 | sexsexagintillion | sexsexagintillion |
| 204 | septensexagintillion | septensexagintillion |
| 207 | octosexagintillion | octosexagintillion |
| 210 | novemsexagintillion | novemsexagintillion |
| 213 | septagintillion | septuagintillion |
| 216 | unseptagintillion | unseptuagintillion |
| 219 | duoseptagintillion | duoseptuagintillion |
| 222 | treseptagintillion | treseptuagintillion |
| 225 | quatorseptagintillion | quattuorseptuagintillion |
| 228 | quinseptagintillion | quinseptuagintillion |
| 231 | sexseptagintillion | sexseptuagintillion |
| 234 | septenseptagintillion | septenseptuagintillion |
| 237 | octoseptagintillion | octoseptuagintillion |
| 240 | novemseptagintillion | novemseptuagintillion |
| 243 | octogintillion | octogintillion |
| 246 | unoctogintillion | unoctogintillion |
| 249 | duooctogintillion | duooctogintillion |
| 252 | tracktogintillion | treoctogintillion |
| 255 | quatoroctogintillion | quattuoroctogintillion |
| 258 | quinoctogintillion | quinoctogintillion |
| 261 | sexoctogintillion | sexoctogintillion |
| 264 | septoktogintillion | septoctogintillion |
| 267 | octoctogintillion | octooctogintillion |
| 270 | novemoctogintillion | novemoctogintillion |
| 273 | nonagintillion | nonagintillion |
| 276 | unnonagintillion | unnonagintillion |
| 279 | duononagintillion | duononagintillion |
| 282 | trenonagintillion | trenonagintillion |
| 285 | quatornonagintillion | quattuornonagintillion |
| 288 | quinnonagintillion | quinnonagintillion |
| 291 | sexnagintillion | sexnonagintillion |
| 294 | septennonagintillion | septennonagintillion |
| 297 | octononagintillion | octononagintillion |
| 300 | novemnonagintillion | novemnonagintillion |
| 303 | sentilyon | sentilyon |
Ano ang pangalan ng pinakamalaking prime number
 Ang isang pangunahing numero ay isa na mahahati sa pamamagitan lamang ng kanyang sarili at ng isa. Sa pagtatapos ng 2018, ipinakita ng Amerikanong si Patrick Laroche ang pinakamalaking punong numero sa pang-agham na mundo.
Ang isang pangunahing numero ay isa na mahahati sa pamamagitan lamang ng kanyang sarili at ng isa. Sa pagtatapos ng 2018, ipinakita ng Amerikanong si Patrick Laroche ang pinakamalaking punong numero sa pang-agham na mundo.
- Ang haba nito ay 24,862,048 na mga character. Para sa paghahambing: sa gawaing paggawa ng epoch ng L.N. Ang "Digmaan at Kapayapaan" ni Tolstoy ay halos 6-7 milyong mga character, kung isasama mo ang bantas at mga puwang.
- Ang numerong ito ay maaaring isulat tulad ng sumusunod: 282589933-1
- At ito ay nababasa nang ganito: dalawa sa lakas na 82589933 na ibinawas ng isa.
- Mayroong isang buong online na proyekto ng GIMPS, na naglalayong eksaktong hanapin ang pinakamalaking mga prima. Nakikilahok dito ang mga matematiko mula sa iba`t ibang mga bansa. Samakatuwid, ang mga bagong may hawak ng record ay madalas na lumilitaw. Ang mga siyentista ay nagtatrabaho, tulad ng sinasabi nila, hindi para sa takot, ngunit para sa pera. Pagkatapos ng lahat, kung sino ang magbubukas ng susunod na pinakamalaking prime ng Mersenne ay makakakuha ng $ 3,000.
Ano ang pinakamalaking bilang sa buong mundo
 Noong 1980, kasama sa Guinness Book of Records ang numero ng Graham (kilala rin bilang G64 o G), na pinangalanang mula sa American matematiko na si Ronald Graham. Ito ang pinakamalaking bilang na ginamit sa isang mahalagang patunay sa matematika. Pinag-uusapan natin ang teorya ni Frank Ramsey.
Noong 1980, kasama sa Guinness Book of Records ang numero ng Graham (kilala rin bilang G64 o G), na pinangalanang mula sa American matematiko na si Ronald Graham. Ito ang pinakamalaking bilang na ginamit sa isang mahalagang patunay sa matematika. Pinag-uusapan natin ang teorya ni Frank Ramsey.
Maikling tungkol sa teoryang ito: isipin ang isang N-dimensional na kubo, ang mga vertex na ito ay random na konektado ng pula o asul na mga segment ng linya. At ang aming gawain ay upang maunawaan hanggang sa anong halaga ng N posible (kung ipininta namin ang mga gilid ng kubo sa iba't ibang paraan), upang maiwasan ang isang sitwasyon kung saan ang isang eroplano sa kubo ay lagyan ng kulay ng isang kulay. Iyon ay, hindi tayo dapat makakuha ng isang kulay na "sobre".
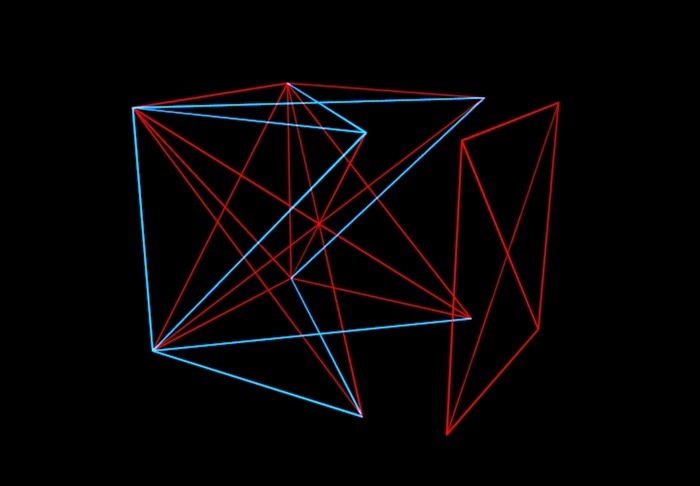
Ang mga matematiko ay nagpinta ng kubo sa ganitong paraan at iyon, naka-out na hanggang sa isang anim na dimensional na kubo, maaari kang makagawa at gawin ang mga linya ng parehong kulay na kumokonekta sa apat na mga vertex ay hindi namamalagi sa parehong eroplano. Ngunit sa pitong-dimensional, tulad ng nalaman nina Graham at Rothschild, ang ganoong trick ay hindi na posible. At may isang walong-dimensional. At ... "at iba pa", kung saan, gayunpaman, ay hindi walang hanggan, ngunit nagtatapos sa isang hindi kapani-paniwala na naglalakihang numero. Ito ang tinatawag nilang numero ni Graham. Sa pamamagitan ng paraan, ang solusyon ni Graham at Rothschild ay hindi na napapanahon. Napag-alaman ng mga matematiko na ang 6-7-8-9-10-11-12-dimensional na mga cube ay maaari pa ring ipinta nang walang mga sobre. Ngunit sa isang lugar sa pagitan ng 13 at numero ni Graham, may garantisadong maging isang numero sa itaas na "mga sobre" ay magkakaroon sa anumang kaso.
Ang bilang ni Graham ay nakakuha ng pagkilala sa buong mundo noong 1977 nang ang kilalang popularidad ng agham na si Martin Gardner ay nagsulat tungkol dito sa Scientific American.
At bagaman mula noon ay may iba pang mga kandidato para sa pamagat ng pinakamaraming bilang sa matematika, ang "brainchild" ni Graham ay ang pinakatanyag at kilalang tao. At kung narinig mo ang tungkol sa "pamilya ng karbon":
- googol - 10100;
O: 10,000,000,000,000,000,000,000,000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 - googolplex - 10googol,
kung gayon dapat mong malaman na ang mga numerong ito sa matematika ay "pagmamasa" lamang, at ang bilang ni Graham ay isang hindi maiisip na bilang ng mga beses na mas malaki kaysa sa kanila. At kahit na higit sa isang numero ng Skuse sa pagitan ng 1019 at 1.3971672 10316 at tinatayang pantay e727,951336108.
Nagtataka, sa pamamagitan ng pag-imbento ng googol, nais ng Amerikanong dalub-agbilang na si Edward Kazner na ipakita sa mga mag-aaral ang pagkakaiba sa pagitan ng isang hindi kapani-paniwalang malaking bilang at kawalang-hanggan. Pagkatapos ang numero ni Graham ay maaaring "pumutok lang ang iyong isip."
Posible bang isipin at isulat ang isang bilang na hindi maunawaan
Hindi masasabi sa iyo ng mga matematiko ang eksaktong bilang ng mga digit sa numero ni Graham, pabayaan ang bilangin sa kanya. Ang huling 50 na digit lamang ng pinakamaraming bilang sa mundo ang kilala - ito ay ... 03222348723967018485186439059104575627262464195387.
Ngunit ang mga numero kung saan nagsisimula ang G64 ay hindi kilala, at malamang na hindi mangyari.
Paghambingin natin ang tatlong halimaw: googol, googolplex, at numero ni Graham.
- Ang Googol ay ang bilang ng mga butil ng buhangin na maaaring magkasya sa uniberso, pinarami ng 10 bilyon.Kaya, isipin ang isang uniberso na puno ng maliliit na butil ng buhangin - sampu-sampung bilyong ilaw na taon sa itaas ng Earth, sa ibaba nito, sa harap nito, sa likuran nito - walang katapusang buhangin.
Ngayon isipin na sa ilang mga punto kumuha ka ng isang butil ng buhangin upang suriin ito sa ilalim ng isang malakas na mikroskopyo. At nakikita mo na sa katunayan hindi lamang ito ang butil, ngunit 10 bilyong mikroskopiko na butil, at magkakasama ang laki ng isang butil ng buhangin. Kung iyon ang kaso para sa bawat solong butil ng buhangin sa hypothetical na uniberso na ito, kung gayon ang kabuuan ng mga mikroskopikong butil na ito ay magiging isang googol.
- Upang mabilang ang googolplex, ang astronomo at astrophysicist na si Carl Sagan ay nagbigay ng isang halimbawa ng pagpuno sa buong dami ng napapansin na uniberso ng mga pinong dust particle na humigit-kumulang na 1.5 micrometers sa laki. Batay dito, ang kabuuang bilang ng magkakaibang mga kumbinasyon kung saan matatagpuan ang mga maliit na butil na ito ay magiging halos katumbas ng isang googolplex.
- Ngayon isipin na ang isang googolplex ay hindi kahit isang butil ng buhangin, ngunit isang maliit na punto na makikita lamang sa pamamagitan ng pinakamakapangyarihang mikroskopyo. At ang aming buong sansinukob ay napuno ng mga maliliit na tuldok. Kaya, kahit na ito ay wala sa anumang paghahambing sa numero ni Graham. Ngunit paano kung nais naming gamitin ang buong puwang ng napapansin na uniberso upang maitala ito (ipagpalagay na ang pag-record ng bawat digit ay tumatagal ng hindi bababa sa dami ng Planck)? Naku, hindi ito gagana para sa atin! Ngunit maaari kang palaging pumunta sa ibang paraan.
Paano isulat ang G64 gamit ang pamamaraan ni Knuth
Noong 1976, iminungkahi ng Amerikanong siyentista na si Donald Knuth ang konsepto ng mga superdegree o notasyon ni Knuth. Ito ay isang pamamaraan na nagbibigay-daan sa iyo upang sumulat ng napakalaking mga numero gamit ang paitaas na mga arrow na tumuturo. Ang pagpapaliban ay ipinahiwatig ng isang pataas na arrow: ↑.
Ito ang hitsura ng notasyong ito: a ↑ b = ab = a × a × a ×…, at iba pa b beses.
- Halimbawa 3 ↑ 3 = 3³.
- Ang Googol ay nakasulat bilang 10 ↑ 10 ↑ 2.
- Isang googolplex - 10 ↑ 10 ↑ 10 ↑ 2
Isang mahalagang tampok ng pataas na arrow ay napakabilis lumaki. Ang pagkakalantad ay lumalaki nang mas mabilis kaysa sa pagpaparami. Ang 2 × 10 ay 20 lamang, ngunit 2 ↑ 10 = 1024. Sa parehong paraan, ang bawat bagong antas ng mga arrow ay lumalaki nang mas mabilis kaysa sa nakaraang antas.
Kung isipin mo ang isang power tower ng triplets na 3 ↑↑↑ 4, makakakuha ka ng isang istraktura mula sa Earth hanggang Mars. Ngunit hindi pa namin naabot ang "ilalim ng hagdan" na hahantong sa numero ni Graham.
Maaari naming ilarawan ang numero ni Graham gamit ang isang malaking hanay ng mga pataas na arrow.
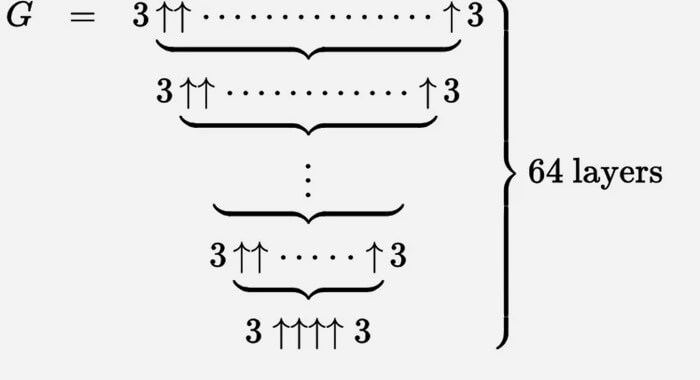
Ito ay pinakamadaling isipin ito bilang isang umuulit na proseso. Nagsisimula kami sa ilalim na may g 1 = 3 ↑↑↑↑ 3, at pagkatapos ay lumikha ng isang pangalawang hilera (tawagan natin itong g 2) na may g 1 na arrow sa pagitan ng mga triplet.
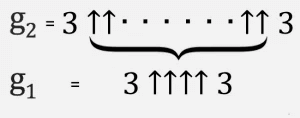
Pagkatapos g 3 ay dalawang triple na pinaghihiwalay ng g 2 na may paitaas na mga arrow at iba pa, hanggang sa g 64 na may g 63 na arrow sa pagitan ng triple ay isang numero ng Graham.
Kung pipiliin mo ang isang habang-buhay na katumbas ng numero ng Graham sa halip na imortalidad, ang resulta ay magiging halos pareho. Kahit na ipalagay natin na ang mga kundisyon sa Uniberso, sa Solar System at sa Lupa ay mananatili magpakailanman na hindi nagbabago, ang utak ng tao ay hindi maaaring tiniis ng gayong mahabang panahon nang walang mapanganib na mga pagbabago.

