On pense que le concept de nombres est né pour la première fois lorsque les préhistoriques ont commencé à utiliser leurs doigts pour compter quelque chose. Depuis lors, l'humanité a parcouru un long chemin. Nous utilisons maintenant des calculatrices et des ordinateurs pour compter les plus grands nombres. Et même des noms sont apparus pour des nombres si grands qu'ils ne peuvent guère être imaginés.
Infini de nombres dénombrables
Il semblerait que la réponse à la question de savoir quel est le plus grand nombre en mathématiques est très simple. Infinity, non? Mais ce n'est pas tout à fait correct. Après tout, l'infini n'est pas du tout un nombre, mais un concept. Idée.
L'infini (infinitum) est un concept qui, en traduction du latin, signifie «sans frontières». La définition de l'infini en mathématiques dit que peu importe la taille d'un nombre, vous pouvez toujours y ajouter 1 et il deviendra plus grand.
Par conséquent, à proprement parler, le plus grand nombre au monde n'existe pas. Vous ne pouvez nommer que le plus grand nombre avec un nom spécifique.
Certains des noms les plus connus pour les grands nombres sont:
| Nombre de zéros | Nom | Nom en anglais |
|---|---|---|
| 3 | mille | mille |
| 6 | million | million |
| 9 | milliard (milliard) | milliard |
| 12 | mille milliards | mille milliards |
| 15 | quadrillion | quadrillion |
| 18 | quintillion | quintillion |
| 21 | sextillion | sextillion |
| 24 | septillion | septillion |
| 27 | octillion | octillion |
| 30 | quintillion | nonillion |
| 33 | décillion | décillion |
| 36 | indécillion | indécillion |
| 39 | duodécillion | duodécillion |
| 42 | tredecillion | tredecillion |
| 45 | quatuorddecillion | quattuordecillion |
| 48 | quindecillion | quindecillion |
| 51 | sexdecillion | sexdecillion |
| 54 | sept millions de dollars | sept millions de dollars |
| 57 | octodécillion | octodécillion |
| 60 | novemdecillion | novemdecillion |
| 63 | vigintillion | vigintillion |
| 66 | unvigintillion | unvigintillion |
| 69 | duovigintillion | duovigintillion |
| 72 | trevigintillion | trevigintillion |
| 75 | quatuorvigintillion | quattuorvigintillion |
| 78 | quinvigintillion | quinvigintillion |
| 81 | sexvigintillion | sexvigintillion |
| 84 | septenvigintillion | septenvigintillion |
| 87 | octovigintillion | octovigintillion |
| 90 | novemvigintillion | novemvigintillion |
| 93 | trigintillion | trigintillion |
| 96 | untrigintillion | untrigintillion |
| 99 | duotrigintillion | duotrigintillion |
| 102 | trétrigintillion | trestrigintillion |
| 105 | quattrigintillion | quattuortrigintillion |
| 108 | quintrigintillion | quintrigintillion |
| 111 | sextrigintillion | sextrigintillion |
| 114 | septentrigintillion | septentrigintillion |
| 117 | octotrigintillion | octotrigintillion |
| 120 | novemtrigintillion | novemtrigintillion |
| 123 | quadragintillion | quadragintillion |
| 126 | unquadragintillion | unquadragintillion |
| 129 | duoquadragintillion | duoquadragintillion |
| 132 | trackquadragintillion | trequadragintillion |
| 135 | quatorquadragintillion | quattuorquadragintillion |
| 138 | quinquadragintillion | quinquadragintillion |
| 141 | sexquadragintillion | sexquadragintillion |
| 144 | septinquadragintillion | septenquadragintillion |
| 147 | octoquadragintillion | octoquadragintillion |
| 150 | novemquadragintillion | novemquadragintillion |
| 153 | quinquagintillion | quinquagintillion |
| 156 | unquincagintillion | unquinquagintillion |
| 159 | duoquincagintillion | duoquinquagintillion |
| 162 | trequincagintillion | trequinquagintillion |
| 165 | quatorquincagintillion | quattuorquinquagintillion |
| 168 | quinquincagintillion | quinquinquagintillion |
| 171 | sexquincagintillion | sexquinquagintillion |
| 174 | septenquincagintillion | septenquinquagintillion |
| 177 | octoquincagintillion | octoquinquagintillion |
| 180 | novemquincagintillion | novemquinquagintillion |
| 183 | sexagintillion | sexagintillion |
| 186 | unsexagintillion | unsexagintillion |
| 189 | duosexagintillion | duosexagintillion |
| 192 | tresexagintillion | tresexagintillion |
| 195 | quatorsexagintillion | quattuorsexagintillion |
| 198 | quinsexagintillion | quinsexagintillion |
| 201 | sexsexagintillion | sexsexagintillion |
| 204 | septensexagintillion | septensexagintillion |
| 207 | octosexagintillion | octosexagintillion |
| 210 | novemsexagintillion | novemsexagintillion |
| 213 | septagintillion | septuagintillion |
| 216 | unseptagintillion | unseptuagintillion |
| 219 | duoseptagintillion | duoseptuagintillion |
| 222 | treseptagintillion | treseptuagintillion |
| 225 | quatorseptagintillion | quattuorseptuagintillion |
| 228 | quinseptagintillion | quinseptuagintillion |
| 231 | sexseptagintillion | sexseptuagintillion |
| 234 | septenseptagintillion | septenseptuagintillion |
| 237 | octoseptagintillion | octoseptuagintillion |
| 240 | novemseptagintillion | novemseptuagintillion |
| 243 | octogintillion | octogintillion |
| 246 | unoctogintillion | unoctogintillion |
| 249 | duooctogintillion | duooctogintillion |
| 252 | tracktogintillion | treoctogintillion |
| 255 | quatoroktogintillion | quattuoroctogintillion |
| 258 | quinoctogintillion | quinoctogintillion |
| 261 | sexoctogintillion | sexoctogintillion |
| 264 | septoktogintillion | septoctogintillion |
| 267 | octoctogintillion | octooctogintillion |
| 270 | novemoctogintillion | novemoctogintillion |
| 273 | nonagintillion | nonagintillion |
| 276 | un milliard de dollars | un milliard de dollars |
| 279 | duononagintillion | duononagintillion |
| 282 | trénonagintillion | trénonagintillion |
| 285 | quatornonagintillion | quattuornonagintillion |
| 288 | quinnonagintillion | quinnonagintillion |
| 291 | sexnagintillion | sexnonagintillion |
| 294 | septennonagintillion | septennonagintillion |
| 297 | octononagintillion | octononagintillion |
| 300 | novemnonagintillion | novemnonagintillion |
| 303 | centillion | centillion |
Quel est le nom du plus grand nombre premier
 Un nombre premier est celui qui n'est divisible que par lui-même et par un. Fin 2018, l'Américain Patrick Laroche a présenté le plus grand nombre premier au monde scientifique.
Un nombre premier est celui qui n'est divisible que par lui-même et par un. Fin 2018, l'Américain Patrick Laroche a présenté le plus grand nombre premier au monde scientifique.
- Sa longueur est de 24 862 048 caractères. À titre de comparaison: dans l'œuvre d'époque de L.N. "Guerre et paix" de Tolstoï compte environ 6 à 7 millions de caractères, si vous incluez la ponctuation et les espaces.
- Ce nombre peut s'écrire comme suit: 282589933-1
- Et cela se lit comme suit: deux à la puissance de 82589933 moins un.
- Il existe tout un projet en ligne GIMPS, visant exactement à trouver les plus grands nombres premiers. Des mathématiciens de différents pays y participent. Par conséquent, de nouveaux détenteurs de records apparaissent fréquemment. Les scientifiques travaillent, comme on dit, non par peur, mais pour de l'argent. Après tout, celui qui ouvrira le prochain plus grand prime de Mersenne recevra 3 000 $.
Quel est le plus grand nombre au monde
 En 1980, le livre Guinness des records incluait le numéro Graham (alias G64 ou G), du nom du mathématicien américain Ronald Graham. C'est le plus grand nombre jamais utilisé dans une preuve mathématique importante. Nous parlons de la théorie de Frank Ramsey.
En 1980, le livre Guinness des records incluait le numéro Graham (alias G64 ou G), du nom du mathématicien américain Ronald Graham. C'est le plus grand nombre jamais utilisé dans une preuve mathématique importante. Nous parlons de la théorie de Frank Ramsey.
En bref sur cette théorie: imaginez un cube à N dimensions, ses sommets sont reliés aléatoirement par des segments de ligne rouge ou bleue. Et notre tâche est de comprendre jusqu'à quelle valeur de N il est possible (si les bords du cube sont peints de différentes manières), pour éviter une situation dans laquelle un plan du cube sera peint avec une couleur. Autrement dit, nous ne devrions pas obtenir une «enveloppe» à une seule couleur.
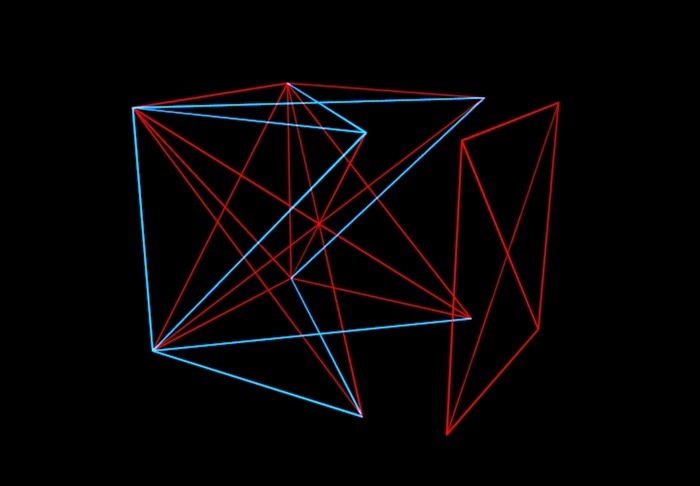
Les mathématiciens ont peint le cube de cette façon et cela, il s'est avéré que jusqu'à un cube à six dimensions, vous pouvez créer et faire en sorte que les lignes de la même couleur reliant les quatre sommets ne se trouvent pas dans le même plan. Mais avec les sept dimensions, comme Graham et Rothschild l'ont découvert, une telle astuce n'est plus possible. Et avec un huit dimensions. Et ... "et ainsi de suite", qui, cependant, n'est pas infini, mais se termine par un nombre fantastiquement gigantesque. C'est ce qu'ils appellent le numéro de Graham. À propos, la solution de Graham et Rothschild est désormais dépassée. Les mathématiciens ont découvert que les cubes de dimensions 6-7-8-9-10-11-12 peuvent toujours être peints sans enveloppe. Mais quelque part entre 13 et le nombre de Graham, il est garanti qu'il y aura un nombre au-dessus duquel les «enveloppes» seront de toute façon.
Le numéro de Graham a gagné une reconnaissance mondiale en 1977 lorsque le célèbre vulgarisateur scientifique Martin Gardner a écrit à ce sujet dans Scientific American.
Et bien que depuis lors, il y ait eu d'autres candidats pour le titre du plus grand nombre en mathématiques, «l'idée originale» de Graham est la plus populaire et la plus connue. Et si vous avez entendu parler de la "famille du charbon":
- googol - 10100;
Ou: 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 - googolplex - 10googol,
alors vous devriez savoir que ces nombres en mathématiques sont juste "pétrissants", et le nombre de Graham est un nombre impensable de fois plus grand qu'eux. Et même plus qu'un numéro Skuse entre 1019 et 1.3971672 10316 et approximativement égal e727,951336108.
Curieusement, en inventant googol, le mathématicien américain Edward Kazner a voulu montrer aux élèves la différence entre un nombre incroyablement grand et l'infini. Alors le numéro de Graham pourrait juste «vous épater».
Est-il possible d'imaginer et d'écrire un nombre incompréhensible
Les mathématiciens ne pourront pas vous dire le nombre exact de chiffres du nombre de Graham, et encore moins compter pour lui. Seuls les 50 derniers chiffres du plus grand nombre au monde sont connus - c'est ... 03222348723967018485186439059104575627262464195387.
Mais les chiffres avec lesquels le G64 commence sont inconnus et ne le seront probablement jamais.
Comparons trois monstres: googol, googolplex et le nombre de Graham.
- Googol est le nombre de grains de sable pouvant tenir dans l'univers, multiplié par 10 milliards.Alors, imaginez un univers rempli de petits grains de sable - des dizaines de milliards d'années-lumière au-dessus de la Terre, en dessous, devant elle, derrière - du sable sans fin.
Imaginez maintenant qu'à un moment donné, vous prenez un grain de sable pour l'examiner sous un microscope puissant. Et vous voyez qu'en fait ce n'est pas le seul grain, mais 10 milliards de grains microscopiques, et tous ensemble, ils ont la taille d'un grain de sable. Si tel était le cas pour chaque grain de sable dans cet univers hypothétique, alors le total de ces grains microscopiques serait un googol.
- Pour quantifier le googolplex, l'astronome et astrophysicien Carl Sagan a donné un exemple de remplissage de tout le volume de l'univers observable avec de fines particules de poussière d'environ 1,5 micromètre. Sur cette base, le nombre total de combinaisons différentes dans lesquelles ces particules peuvent être localisées sera approximativement égal à un googolplex.
- Imaginons maintenant qu'un googolplex n'est même pas un grain de sable, mais un minuscule point qui ne peut être vu qu'à travers le microscope le plus puissant. Et tout notre univers est rempli de si petits points. Donc, même cela n'est pas comparable au nombre de Graham. Mais que se passe-t-il si nous voulons utiliser tout l'espace de l'univers observable pour l'enregistrer (supposons que l'enregistrement de chaque chiffre occupe au moins le volume de Planck)? Hélas, cela ne fonctionnera pas pour nous! Mais vous pouvez toujours aller dans l'autre sens.
Comment écrire G64 en utilisant la méthode de Knuth
En 1976, le scientifique américain Donald Knuth a proposé le concept de super degrés ou la notation de Knuth. C'est une méthode qui vous permet d'écrire de très grands nombres à l'aide des flèches pointant vers le haut. L'exponentiation est indiquée par une flèche pointant vers le haut: ↑.
Voici à quoi ressemble cette notation: a ↑ b = ab = a × a × a ×…, et ainsi de suite b fois.
- Par exemple 3 ↑ 3 = 3³.
- Googol s'écrit 10 ↑ 10 ↑ 2.
- Un googolplex - 10 ↑ 10 ↑ 10 ↑ 2
Une caractéristique importante des flèches vers le haut est qu'elles poussent très rapidement. L'exposition croît beaucoup plus vite que la multiplication. 2 × 10 est seulement 20, mais 2 ↑ 10 = 1024. De la même manière, chaque nouveau niveau de flèches croît beaucoup plus vite que le niveau précédent.
Si vous imaginez mentalement une tour de puissance de triplés 3 ↑↑↑ 4, vous obtiendrez une structure de taille allant de la Terre à Mars. Mais nous n'avons même pas atteint le «dernier échelon» qui nous mène au nombre de Graham.
Nous pouvons décrire le nombre de Graham avec un ensemble énorme de ces flèches vers le haut.
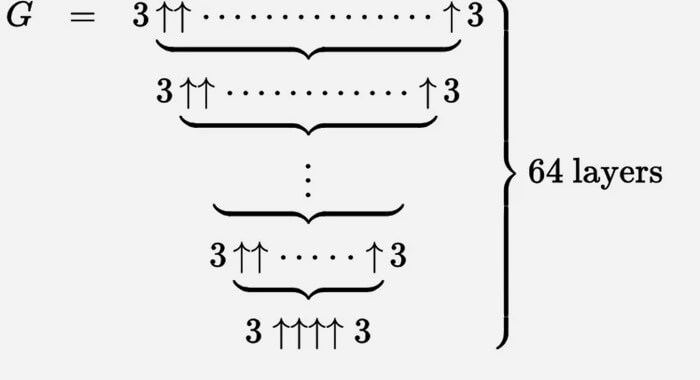
Il est plus facile de considérer cela comme un processus itératif. Nous commençons en bas avec g 1 = 3 ↑↑↑↑ 3, puis créons une deuxième ligne (appelons-la g 2) avec des flèches g 1 entre les triplets.
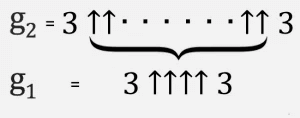
Alors g 3 est deux triplets séparés par g 2 avec des flèches vers le haut et ainsi de suite, jusqu'à ce que g 64 avec g 63 flèches entre les triplets soit un nombre de Graham.
Si vous choisissez une durée de vie égale au nombre de Graham au lieu de l'immortalité, le résultat sera presque le même. Même si nous supposons que les conditions dans l'Univers, dans le système solaire et sur Terre resteront à jamais inchangées, le cerveau humain n'aurait pas pu endurer une si longue période de temps sans changements nocifs.

