Uważa się, że koncepcja liczb powstała, gdy prehistoryczni ludzie zaczęli liczyć coś palcami. Od tego czasu ludzkość przeszła długą drogę. Teraz używamy kalkulatorów i komputerów do liczenia największych liczb. Pojawiły się nawet nazwy liczb, które są tak duże, że trudno je sobie wyobrazić.
Nieskończoność policzalnych liczb
Wydawałoby się, że odpowiedź na pytanie, jaka jest największa liczba w matematyce, jest bardzo prosta. Nieskończoność, prawda? Ale to nie jest całkowicie poprawne. W końcu nieskończoność nie jest wcale liczbą, ale pojęciem. Pomysł.
Nieskończoność (infinitum) to pojęcie, które w tłumaczeniu z łaciny oznacza „bez granic”. Definicja nieskończoności w matematyce mówi, że bez względu na to, jak duża jest liczba, zawsze możesz dodać do niej 1, a będzie rosła.
Dlatego, mówiąc ściśle, nie ma czegoś takiego jak największa liczba na świecie. Możesz podać tylko największą liczbę, podając określoną nazwę.
Niektóre z bardziej znanych nazw dużych liczb to:
| Liczba zer | Nazwa | Imię w języku angielskim |
|---|---|---|
| 3 | tysiąc | tysiąc |
| 6 | milion | milion |
| 9 | miliard (miliard) | miliard |
| 12 | kwintylion | kwintylion |
| 15 | kwadrylion | kwadrylion |
| 18 | kwintylionów | kwintylionów |
| 21 | sextillion | sextillion |
| 24 | septillion | septillion |
| 27 | oktylion | oktylion |
| 30 | kwintylionów | nonillion |
| 33 | decylionów | decylionów |
| 36 | undecillion | undecillion |
| 39 | duodecillion | duodecillion |
| 42 | tredecillion | tredecillion |
| 45 | quatuorddecillion | quattuordecillion |
| 48 | quindecillion | quindecillion |
| 51 | sexdecillion | sexdecillion |
| 54 | septendecillion | septendecillion |
| 57 | octodecillion | octodecillion |
| 60 | novemdecillion | novemdecillion |
| 63 | vigintillion | vigintillion |
| 66 | unvigintillion | unvigintillion |
| 69 | duovigintillion | duovigintillion |
| 72 | trevigintillion | trevigintillion |
| 75 | quatuorvigintillion | quattuorvigintillion |
| 78 | quinvigintillion | quinvigintillion |
| 81 | sexvigintillion | sexvigintillion |
| 84 | septenvigintillion | septenvigintillion |
| 87 | octovigintillion | octovigintillion |
| 90 | novemvigintillion | novemvigintillion |
| 93 | trigintillion | trigintillion |
| 96 | untrigintillion | untrigintillion |
| 99 | duotrigintillion | duotrigintillion |
| 102 | tretrigintillion | trestrigintillion |
| 105 | quattrigintillion | quattuortrigintillion |
| 108 | quintrigintillion | quintrigintillion |
| 111 | sextrigintillion | sextrigintillion |
| 114 | septentrigintillion | septentrigintillion |
| 117 | octotrigintillion | octotrigintillion |
| 120 | novemtrigintillion | novemtrigintillion |
| 123 | quadragintillion | quadragintillion |
| 126 | unquadragintillion | unquadragintillion |
| 129 | duoquadragintillion | duoquadragintillion |
| 132 | trackquadragintillion | trequadragintillion |
| 135 | quatorquadragintillion | quattuorquadragintillion |
| 138 | quinquadragintillion | quinquadragintillion |
| 141 | sexquadragintillion | sexquadragintillion |
| 144 | septinquadragintillion | septenquadragintillion |
| 147 | octoquadragintillion | octoquadragintillion |
| 150 | novemquadragintillion | novemquadragintillion |
| 153 | quinquagintillion | quinquagintillion |
| 156 | unquincagintillion | unquinquagintillion |
| 159 | duoquincagintillion | duoquinquagintillion |
| 162 | trequincagintillion | trequinquagintillion |
| 165 | quatorquincagintillion | quattuorquinquagintillion |
| 168 | quinquincagintillion | quinquinquagintillion |
| 171 | sexquincagintillion | sexquinquagintillion |
| 174 | septenquincagintillion | septenquinquagintillion |
| 177 | octoquincagintillion | octoquinquagintillion |
| 180 | novemquincagintillion | novemquinquagintillion |
| 183 | sexagintillion | sexagintillion |
| 186 | unsexagintillion | unsexagintillion |
| 189 | duosexagintillion | duosexagintillion |
| 192 | tresexagintillion | tresexagintillion |
| 195 | quatorsexagintillion | quattuorsexagintillion |
| 198 | quinsexagintillion | quinsexagintillion |
| 201 | sexsexagintillion | sexsexagintillion |
| 204 | septensexagintillion | septensexagintillion |
| 207 | octosexagintillion | octosexagintillion |
| 210 | novemsexagintillion | novemsexagintillion |
| 213 | septagintillion | septuagintillion |
| 216 | unseptagintillion | unseptuagintillion |
| 219 | duoseptagintillion | duoseptuagintillion |
| 222 | treseptagintillion | treseptuagintillion |
| 225 | quatorseptagintillion | quattuorseptuagintillion |
| 228 | quinseptagintillion | quinseptuagintillion |
| 231 | sexseptagintillion | sexseptuagintillion |
| 234 | septenseptagintillion | septenseptuagintillion |
| 237 | octoseptagintillion | octoseptuagintillion |
| 240 | novemseptagintillion | novemseptuagintillion |
| 243 | octogintillion | octogintillion |
| 246 | unoctogintillion | unoctogintillion |
| 249 | duooctogintillion | duooctogintillion |
| 252 | tracktogintillion | treoctogintillion |
| 255 | quatoroctogintillion | quattuoroctogintillion |
| 258 | quinoctogintillion | quinoctogintillion |
| 261 | sexoctogintillion | sexoctogintillion |
| 264 | septoktogintillion | septoctogintillion |
| 267 | octoctogintillion | octooctogintillion |
| 270 | novemoctogintillion | novemoctogintillion |
| 273 | nonagintillion | nonagintillion |
| 276 | unnonagintillion | unnonagintillion |
| 279 | duononagintillion | duononagintillion |
| 282 | trenonagintillion | trenonagintillion |
| 285 | quatornonagintillion | quattuornonagintillion |
| 288 | quinnonagintillion | quinnonagintillion |
| 291 | sexnagintillion | sexnonagintillion |
| 294 | septennonagintillion | septennonagintillion |
| 297 | octononagintillion | octononagintillion |
| 300 | novemnonagintillion | novemnonagintillion |
| 303 | centylionów | centylionów |
Jaka jest nazwa największej liczby pierwszej
 Liczba pierwsza to taka, która jest podzielna tylko przez siebie i przez jeden. Pod koniec 2018 roku Amerykanin Patrick Laroche przedstawił światu naukowemu największą liczbę pierwszą.
Liczba pierwsza to taka, która jest podzielna tylko przez siebie i przez jeden. Pod koniec 2018 roku Amerykanin Patrick Laroche przedstawił światu naukowemu największą liczbę pierwszą.
- Jego długość to 24 862 048 znaków. Dla porównania: w epokowej pracy L.N. „Wojna i pokój” Tołstoja ma około 6-7 milionów znaków, jeśli uwzględnisz znaki interpunkcyjne i spacje.
- Liczbę tę można zapisać w następujący sposób: 282589933-1
- I brzmi tak: dwa do potęgi 82589933 minus jeden.
- Istnieje cały projekt internetowy GIMPS, którego celem jest właśnie znalezienie największych liczb pierwszych. Biorą w nim udział matematycy z różnych krajów. Dlatego często pojawiają się nowi rekordziści. Naukowcy pracują, jak mówią, nie ze strachu, ale dla pieniędzy. W końcu ten, kto otworzy kolejną największą prime Mersenne, otrzyma 3000 $.
Jaka jest największa liczba na świecie
 W 1980 roku Księga Rekordów Guinnessa zawierała numer Grahama (jest to również G64 lub G), nazwany na cześć amerykańskiego matematyka Ronalda Grahama. Jest to największa liczba kiedykolwiek użyta w ważnym dowodzie matematycznym. Mówimy o teorii Franka Ramseya.
W 1980 roku Księga Rekordów Guinnessa zawierała numer Grahama (jest to również G64 lub G), nazwany na cześć amerykańskiego matematyka Ronalda Grahama. Jest to największa liczba kiedykolwiek użyta w ważnym dowodzie matematycznym. Mówimy o teorii Franka Ramseya.
Krótko o tej teorii: wyobraź sobie N-wymiarowy sześcian, którego wierzchołki są losowo połączone czerwonymi lub niebieskimi odcinkami linii. A naszym zadaniem jest zrozumienie, do jakiej wartości N jest to możliwe (jeśli krawędzie sześcianu są pomalowane na różne sposoby), aby uniknąć sytuacji, w której jedna płaszczyzna w sześcianie zostanie pomalowana na jeden kolor. Oznacza to, że nie powinniśmy dostawać jednokolorowej „koperty”.
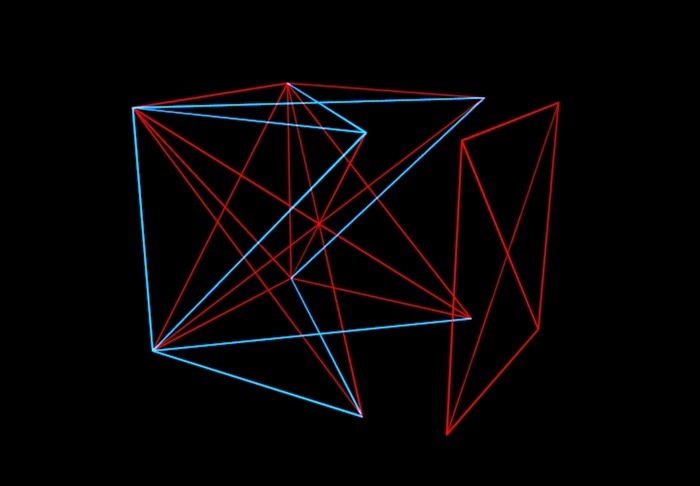
Matematycy pomalowali sześcian w ten sposób i okazało się, że do sześciowymiarowej kostki można wymyślić i sprawić, że linie tego samego koloru łączące cztery wierzchołki nie leżą na tej samej płaszczyźnie. Ale z siedmiowymiarami, jak odkryli Graham i Rothschild, taka sztuczka nie jest już możliwa. I z ośmiowymiarowymi. I… „i tak dalej”, co jednak nie jest nieskończone, ale kończy się fantastycznie gigantyczną liczbą. Tak nazywają numer Grahama. Nawiasem mówiąc, rozwiązanie autorstwa Grahama i Rothschilda jest teraz przestarzałe. Matematycy odkryli, że sześciany o wymiarach 6-7-8-9-10-11-12 można nadal malować bez „kopert”. Ale gdzieś pomiędzy 13 a liczbą Grahama istnieje pewna liczba, powyżej której i tak będą znajdować się „koperty”.
Liczba Grahama zyskała światowe uznanie w 1977 roku, kiedy napisał o niej w Scientific American znany popularyzator nauki Martin Gardner.
I choć od tamtej pory do tytułu największej liczby w matematyce pojawili się inni kandydaci, „pomysł” Grahama jest najpopularniejszy i najbardziej znany. A jeśli słyszałeś o „rodzinie węglowej”:
- googol - 10100;
Lub: 10000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 - googolplex - 10googol,
wtedy powinieneś wiedzieć, że te liczby w matematyce są tylko „ugniataniem”, a liczba Grahama jest niewyobrażalna liczba razy większa od nich. A nawet więcej niż numer Skuse między 1019 i 1,3971672 10316 iw przybliżeniu równe mi727,951336108.
Co ciekawe, wymyślając googol, amerykański matematyk Edward Kasner chciał pokazać uczniom różnicę między niewiarygodnie dużą liczbą a nieskończonością. Wtedy numer Grahama może po prostu „zaskoczyć”.
Czy można sobie wyobrazić i zapisać niezrozumiałą liczbę
Matematycy nie będą w stanie podać dokładnej liczby cyfr w liczbie Grahama, nie mówiąc już o policzeniu do niego. Znanych jest tylko 50 ostatnich cyfr największej liczby na świecie - jest to ... 03222348723967018485186439059104575627262464195387.
Ale liczby, od których zaczyna się G64, są nieznane i prawdopodobnie nigdy nie będą.
Porównajmy trzy potwory: googol, googolplex i liczbę Grahama.
- Googol to liczba ziaren piasku, które mogą zmieścić się we wszechświecie, pomnożona przez 10 miliardów.Wyobraź sobie więc wszechświat pełen małych ziarenek piasku - dziesiątki miliardów lat świetlnych nad Ziemią, pod nią, przed nią, za nią - nieskończony piasek.
Teraz wyobraź sobie, że w pewnym momencie bierzesz jedno ziarenko piasku, aby zbadać je pod silnym mikroskopem. I widzicie, że w rzeczywistości nie jest to pojedyncze ziarno, ale 10 miliardów mikroskopijnych ziaren, które razem mają wielkość ziarenka piasku. Gdyby tak było w przypadku każdego pojedynczego ziarenka piasku w tym hipotetycznym wszechświecie, to suma tych mikroskopijnych ziaren byłaby googolem.
- Aby określić ilościowo googolplex, astronom i astrofizyk Carl Sagan podał przykład wypełnienia całej objętości obserwowalnego Wszechświata drobnymi cząstkami pyłu o wielkości około 1,5 mikrometra. Na tej podstawie całkowita liczba różnych kombinacji, w których te cząstki mogą się znajdować, będzie w przybliżeniu równa jednemu googolpleksowi.
- Teraz wyobraźmy sobie, że googolplex nie jest nawet ziarnkiem piasku, ale maleńkim punktem, który można obejrzeć tylko przez najpotężniejszy mikroskop. A cały nasz wszechświat jest wypełniony takimi maleńkimi kropkami. Więc nawet to nie jest porównywalne z liczbą Grahama. Ale co, jeśli chcemy wykorzystać całą przestrzeń obserwowalnego wszechświata, aby go zarejestrować (przypuśćmy, że zapis każdej cyfry zajmuje co najmniej objętość Plancka)? Niestety, to nie zadziała! Ale zawsze możesz pójść w drugą stronę.
Jak napisać G64 metodą Knutha
W 1976 roku amerykański naukowiec Donald Knuth zaproponował koncepcję super stopni lub notację Knutha. Jest to metoda, która umożliwia wpisywanie bardzo dużych liczb za pomocą strzałek skierowanych w górę. Potęgowanie jest wskazywane przez jedną strzałkę w górę: ↑.
Oto jak wygląda ten zapis: a ↑ b = ab = a × a × a ×… i tak dalej b razy.
- Na przykład 3 ↑ 3 = 3³.
- Googol jest zapisywane jako 10 ↑ 10 ↑ 2.
- Googolplex - 10 ↑ 10 ↑ 10 ↑ 2
Ważną cechą strzałek w górę jest to, że rosną bardzo szybko. Ekspozycja rośnie znacznie szybciej niż mnożenie. 2 × 10 to tylko 20, ale 2 ↑ 10 = 1024. W ten sam sposób każdy nowy poziom strzał rośnie znacznie szybciej niż poprzedni poziom.
Jeśli wyobrazisz sobie w myślach wieżę energetyczną składającą się z trojaczków 3 ↑ Przejdź na 4, otrzymasz strukturę o rozmiarach od Ziemi po Marsa. Ale nie dotarliśmy nawet do „najniższego szczebla”, który prowadzi nas do liczby Grahama.
Liczbę Grahama możemy opisać ogromnym zestawem tych strzałek skierowanych w górę.
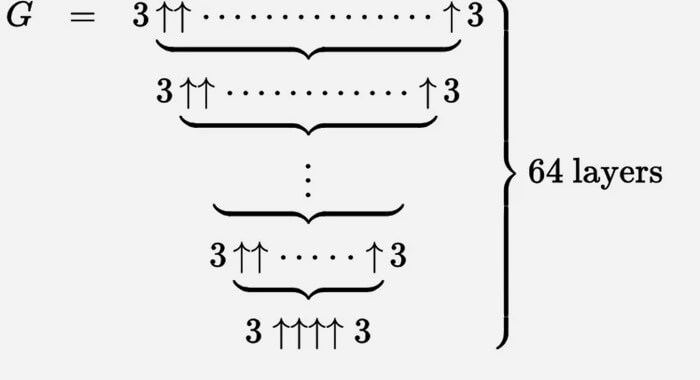
Najłatwiej jest myśleć o tym jako o procesie iteracyjnym. Zaczynamy od dołu od g 1 = 3 ↑ ↑ a następnie tworzymy drugi rząd (nazwijmy to g 2) ze strzałkami g 1 między trojaczkami.
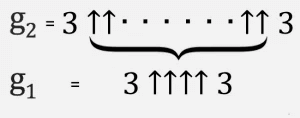
Wtedy g 3 to dwie trójki, oddzielone przez g 2 strzałkami skierowanymi w górę, i tak dalej, aż g 64 z g 63 strzałkami między trójkami będzie liczbą Grahama.
Jeśli zamiast nieśmiertelności wybierzesz długość życia równą liczbie Grahama, wynik będzie prawie taki sam. Nawet jeśli przyjmiemy, że warunki we Wszechświecie, w Układzie Słonecznym i na Ziemi pozostaną na zawsze niezmienione, ludzki mózg nie wytrzymałby tak długiego czasu bez szkodliwych zmian.

