Er wordt aangenomen dat het concept van getallen voor het eerst ontstond toen prehistorische mensen hun vingers begonnen te gebruiken om iets te tellen. Sindsdien heeft de mensheid een lange weg afgelegd. We gebruiken nu rekenmachines en computers om de grootste getallen te tellen. En er zijn zelfs namen verschenen voor nummers die zo groot zijn dat ze nauwelijks kunnen worden voorgesteld.
Oneindigheid van telbare getallen
Het lijkt erop dat het antwoord op de vraag wat het grootste getal in de wiskunde is, heel eenvoudig is. Oneindigheid, toch? Maar dit is niet helemaal correct. Oneindigheid is immers helemaal geen getal, maar een concept. Idee.
Oneindigheid (oneindig) is een concept dat in vertaling uit het Latijn "zonder grenzen" betekent. De definitie van oneindigheid in de wiskunde zegt dat hoe groot een getal ook is, je er altijd 1 bij kunt optellen en het wordt groter.
Strikt genomen bestaat er daarom niet zoiets als het grootste aantal ter wereld. U kunt alleen het grootste nummer noemen met een specifieke naam.
Enkele van de meer bekende namen voor grote aantallen zijn:
| Aantal nullen | Naam | Naam in het Engels |
|---|---|---|
| 3 | duizend | duizend |
| 6 | miljoen | miljoen |
| 9 | miljard (miljard) | miljard |
| 12 | biljoen | biljoen |
| 15 | quadriljoen | quadriljoen |
| 18 | triljoen | triljoen |
| 21 | sextiljoen | sextiljoen |
| 24 | septillion | septillion |
| 27 | octillion | octillion |
| 30 | triljoen | nonillion |
| 33 | deciljoen | deciljoen |
| 36 | undecillion | undecillion |
| 39 | duodecillion | duodecillion |
| 42 | tredecillion | tredecillion |
| 45 | quatuorddecillion | quattuordecillion |
| 48 | quindecillion | quindecillion |
| 51 | sexdecillion | sexdecillion |
| 54 | septendecillion | septendecillion |
| 57 | octodecillion | octodecillion |
| 60 | novemdecillion | novemdecillion |
| 63 | vigintillion | vigintillion |
| 66 | unvigintillion | unvigintillion |
| 69 | duovigintillion | duovigintillion |
| 72 | trevigintillion | trevigintillion |
| 75 | quatuorvigintillion | quattuorvigintillion |
| 78 | quinvigintillion | quinvigintillion |
| 81 | sexvigintillion | sexvigintillion |
| 84 | septenvigintillion | septenvigintillion |
| 87 | octovigintillion | octovigintillion |
| 90 | novemvigintillion | novemvigintillion |
| 93 | triljoen | triljoen |
| 96 | untrigintillion | untrigintillion |
| 99 | duotrigintillion | duotrigintillion |
| 102 | tretrigintillion | trestrigintillion |
| 105 | quattrigintillion | quattuortrigintillion |
| 108 | quintrigintillion | quintrigintillion |
| 111 | sextrigintiljoen | sextrigintiljoen |
| 114 | septentrigintiljoen | septentrigintiljoen |
| 117 | octotrigintillion | octotrigintillion |
| 120 | novemtrigintillion | novemtrigintillion |
| 123 | quadragintillion | quadragintillion |
| 126 | unquadragintillion | unquadragintillion |
| 129 | duoquadragintillion | duoquadragintillion |
| 132 | trackquadragintillion | trequadragintillion |
| 135 | quatorquadragintillion | quattuorquadragintillion |
| 138 | quinquadragintillion | quinquadragintillion |
| 141 | sexquadragintillion | sexquadragintillion |
| 144 | septinquadragintillion | zevenquadragintiljoen |
| 147 | octoquadragintillion | octoquadragintillion |
| 150 | novemquadragintillion | novemquadragintillion |
| 153 | quinquagintillion | quinquagintillion |
| 156 | unquincagintillion | unquinquagintillion |
| 159 | duoquincagintillion | duoquinquagintillion |
| 162 | trequincagintillion | trequinquagintillion |
| 165 | quatorquincagintillion | quattuorquinquagintillion |
| 168 | quinquincagintillion | quinquinquagintillion |
| 171 | sexquincagintillion | sexquinquagintillion |
| 174 | zevenvijftig miljoen | septenquinquagintillion |
| 177 | octoquincagintillion | octoquinquagintillion |
| 180 | novemquincagintillion | novemquinquagintillion |
| 183 | sexagintillion | sexagintillion |
| 186 | unsexagintillion | unsexagintillion |
| 189 | duosexagintillion | duosexagintillion |
| 192 | tresexagintillion | tresexagintillion |
| 195 | quatorsexagintillion | quattuorsexagintillion |
| 198 | quinsexagintillion | quinsexagintillion |
| 201 | sexsexagintillion | sexsexagintillion |
| 204 | septensexagintillion | septensexagintillion |
| 207 | octosexagintillion | octosexagintillion |
| 210 | novemsexagintillion | novemsexagintillion |
| 213 | septagintillion | septuagintillion |
| 216 | unseptagintillion | unseptuagintillion |
| 219 | duoseptagintillion | duoseptuagintillion |
| 222 | treseptagintillion | treseptuagintillion |
| 225 | quatorseptagintillion | quattuorseptuagintillion |
| 228 | quinseptagintillion | quinseptuagintillion |
| 231 | sexseptagintillion | sexseptuagintillion |
| 234 | septenseptagintiljoen | septenseptuagintiljoen |
| 237 | octoseptagintillion | octoseptuagintillion |
| 240 | novemseptagintillion | novemseptuagintillion |
| 243 | octogintillion | octogintillion |
| 246 | unoctogintillion | unoctogintillion |
| 249 | duooctogintillion | duooctogintillion |
| 252 | tracktogintillion | treoctogintillion |
| 255 | quatoroktogintillion | quattuoroctogintillion |
| 258 | quinoctogintillion | quinoctogintillion |
| 261 | sexoctogintillion | sexoctogintillion |
| 264 | septoktogintillion | septoctogintillion |
| 267 | octoctogintillion | octooctogintillion |
| 270 | novemoctogintillion | novemoctogintillion |
| 273 | nonagintillion | nonagintillion |
| 276 | unonagintillion | unonagintillion |
| 279 | duononagintillion | duononagintillion |
| 282 | trenonagintillion | trenonagintillion |
| 285 | quatornonagintillion | quattuornonagintillion |
| 288 | quinnonagintillion | quinnonagintillion |
| 291 | sexnagintillion | sexnonagintillion |
| 294 | septennonagintillion | septennonagintillion |
| 297 | octononagintillion | octononagintillion |
| 300 | novemnonagintillion | novemnonagintillion |
| 303 | centillion | centillion |
Wat is de naam van het grootste priemgetal
 Een priemgetal is er een die alleen door zichzelf en door één deelbaar is. Eind 2018 presenteerde de Amerikaan Patrick Laroche het grootste priemgetal aan de wetenschappelijke wereld.
Een priemgetal is er een die alleen door zichzelf en door één deelbaar is. Eind 2018 presenteerde de Amerikaan Patrick Laroche het grootste priemgetal aan de wetenschappelijke wereld.
- De lengte is 24.862.048 tekens. Ter vergelijking: in het baanbrekende werk van L.N. Tolstoj's "Oorlog en vrede" telt ongeveer 6-7 miljoen tekens, als je leestekens en spaties opneemt.
- Dit nummer kan als volgt worden geschreven: 282589933-1
- En het leest als volgt: twee tot de macht van 82589933 min één.
- Er is een heel online project GIMPS, precies gericht op het vinden van de grootste prime-lenzen. Wiskundigen uit verschillende landen nemen eraan deel. Daarom verschijnen er regelmatig nieuwe recordhouders. Wetenschappers werken, zoals ze zeggen, niet uit angst, maar voor geld. Immers, degene die de volgende hoogste Mersenne prime opent, krijgt $ 3.000.
Wat is het grootste aantal ter wereld
 In 1980 bevatte het Guinness Book of Records het Graham-nummer (ook bekend als G64 of G), genoemd naar de Amerikaanse wiskundige Ronald Graham. Het is het grootste aantal dat ooit is gebruikt in een belangrijk wiskundig bewijs. We hebben het over de theorie van Frank Ramsey.
In 1980 bevatte het Guinness Book of Records het Graham-nummer (ook bekend als G64 of G), genoemd naar de Amerikaanse wiskundige Ronald Graham. Het is het grootste aantal dat ooit is gebruikt in een belangrijk wiskundig bewijs. We hebben het over de theorie van Frank Ramsey.
Kort over deze theorie: stel je een N-dimensionale kubus voor, de hoekpunten zijn willekeurig verbonden door rode of blauwe lijnsegmenten. En onze taak is om te begrijpen tot welke waarde van N het mogelijk is (als we op verschillende manieren over de randen van de kubus schilderen), om een situatie te vermijden waarin één vlak in de kubus met één kleur wordt geverfd. Dat wil zeggen, we zouden geen eenkleurige "envelop" moeten krijgen.
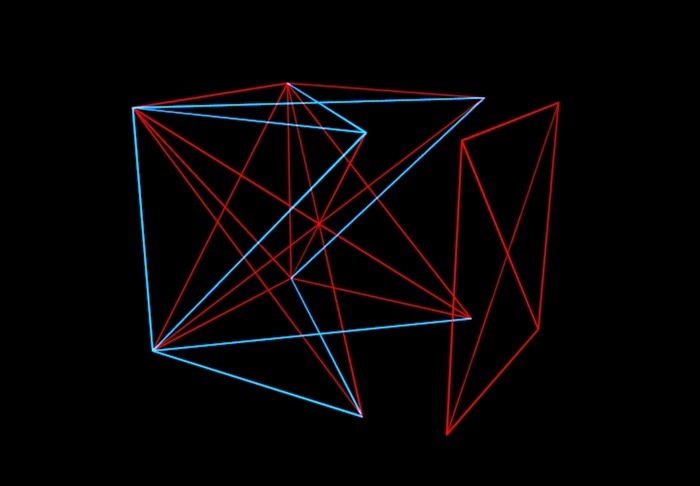
Wiskundigen hebben de kubus op deze manier geschilderd en het bleek dat je tot aan een zesdimensionale kubus de lijnen van dezelfde kleur kunt bedenken en maken die de vier hoekpunten verbinden, niet in hetzelfde vlak liggen. Maar met het zevendimensionale, zoals Graham en Rothschild ontdekten, is zo'n truc niet langer mogelijk. En met een achtdimensionaal. En ... "en ga zo maar door", dat echter niet oneindig is, maar eindigt met een fantastisch gigantisch aantal. Dit is wat ze Grahams nummer noemen. Overigens is de oplossing van Graham en Rothschild inmiddels achterhaald. Wiskundigen hebben ontdekt dat 6-7-8-9-10-11-12-dimensionale kubussen nog steeds kunnen worden geverfd zonder enveloppen. Maar ergens tussen 13 en Graham's nummer is er gegarandeerd een nummer waarboven in ieder geval "enveloppen" zullen zijn.
Graham's nummer kreeg wereldwijde erkenning in 1977 toen de beroemde wetenschapper Martin Gardner erover schreef in Scientific American.
En hoewel er sindsdien andere kandidaten zijn voor de titel van het grootste aantal in de wiskunde, is Grahams "geesteskind" het populairst en bekendst. En als je hebt gehoord over de "kolenfamilie":
- googol - 10100;
Of: 100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 - googolplex - 10googol,
dan zou je moeten weten dat deze getallen in de wiskunde gewoon "kneden" zijn, en dat het getal van Graham een ondenkbaar aantal keer groter is dan zij. En zelfs meer dan een Skuse-getal tussen 1019 en 1.3971672 10316 en ongeveer gelijk e727,951336108.
Vreemd genoeg wilde de Amerikaanse wiskundige Edward Kazner, door googol uit te vinden, studenten het verschil laten zien tussen een ongelooflijk groot aantal en oneindigheid. Dan kan Grahams nummer je gewoon "verbazen".
Is het mogelijk om een onvoorstelbaar getal voor te stellen en op te schrijven?
Wiskundigen zullen je niet het exacte aantal cijfers in Grahams nummer kunnen vertellen, laat staan tot hem tellen. Alleen de laatste 50 cijfers van het grootste nummer ter wereld zijn bekend - dit is ... 03222348723967018485186439059104575627262464195387.
Maar de cijfers waarmee de G64 begint, zijn onbekend en zullen dat waarschijnlijk ook nooit worden.
Laten we drie monsters vergelijken: googol, googolplex en Graham's nummer.
- Googol is het aantal zandkorrels dat in het universum past, vermenigvuldigd met 10 miljard.Stel je dus een universum voor dat gevuld is met kleine zandkorrels - tientallen miljarden lichtjaren boven de aarde, eronder, ervoor, erachter - eindeloos zand.
Stel je nu voor dat je op een gegeven moment een zandkorrel neemt om het onder een krachtige microscoop te onderzoeken. En je ziet dat dit in feite geen enkele korrel is, maar 10 miljard microscopisch kleine korrels, en samen zijn ze zo groot als een zandkorrel. Als dat het geval zou zijn voor elke zandkorrel in dit hypothetische universum, dan zou het totaal van deze microscopisch kleine korrels een googol zijn.
- Om de googolplex te kwantificeren, gaf astronoom en astrofysicus Carl Sagan een voorbeeld van het vullen van het volledige volume van het waarneembare universum met fijne stofdeeltjes van ongeveer 1,5 micrometer groot. Op basis hiervan zal het totale aantal verschillende combinaties waarin deze deeltjes kunnen worden gelokaliseerd ongeveer gelijk zijn aan één googolplex.
- Laten we ons nu eens voorstellen dat een googolplex niet eens een zandkorrel is, maar een klein puntje dat alleen door de krachtigste microscoop kan worden bekeken. En ons hele universum is gevuld met zulke kleine puntjes. Dus zelfs dit is niet vergelijkbaar met het nummer van Graham. Maar wat als we alle ruimte van het waarneembare universum willen gebruiken om het op te nemen (stel dat het opnemen van elk cijfer minstens het Planck-volume in beslag neemt)? Helaas zal dit voor ons niet werken! Maar je kunt altijd de andere kant op gaan.
Hoe G64 te schrijven met de methode van Knuth
In 1976 stelde de Amerikaanse wetenschapper Donald Knuth het concept van superdegrees of de notatie van Knuth voor. Dit is een methode waarmee u zeer grote getallen kunt schrijven met de naar boven wijzende pijlen. Exponentiatie wordt aangegeven door een pijl omhoog: ↑.
Zo ziet deze notatie eruit: a ↑ b = ab = a × a × a ×…, enzovoort, b keer.
- Bijvoorbeeld 3 ↑ 3 = 3³.
- Googol wordt geschreven als 10 ↑ 10 ↑ 2.
- Een googolplex - 10 ↑ 10 ↑ 10 ↑ 2
Een belangrijk kenmerk van de pijlen omhoog is dat ze erg snel groeien. De belichting groeit veel sneller dan de vermenigvuldiging. 2 × 10 is slechts 20, maar 2 ↑ 10 = 1024. Op dezelfde manier groeit elk nieuw niveau van pijlen veel sneller dan het vorige niveau.
Als je je mentaal een krachttoren van drieling 3 ↑↑↑ 4 voorstelt, krijg je een structuur die in grootte varieert van de aarde tot Mars. Maar we hebben nog niet eens de "onderste sport" bereikt die ons naar Grahams nummer leidt.
We kunnen Grahams nummer beschrijven met een enorme reeks van deze opwaartse pijlen.
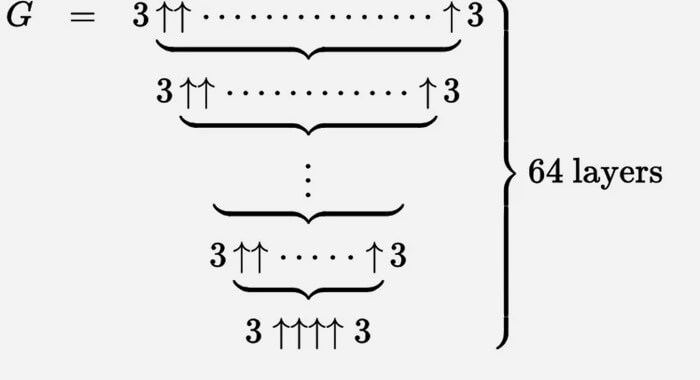
Het is het gemakkelijkst om dit als een iteratief proces te beschouwen. We beginnen onderaan met g 1 = 3 ↑↑↑↑ 3, en maken dan een tweede rij (laten we het g 2 noemen) met g 1 pijlen tussen de tripletten.
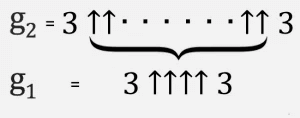
Dan is g 3 twee triples gescheiden door g 2 met opwaartse pijlen enzovoort, totdat g 64 met g 63 pijlen tussen de triples een Graham-getal is.
Als je een levensduur kiest die gelijk is aan het Graham-getal in plaats van onsterfelijkheid, zal het resultaat bijna hetzelfde zijn. Zelfs als we aannemen dat de omstandigheden in het heelal, in het zonnestelsel en op aarde voor altijd ongewijzigd zullen blijven, zou het menselijk brein zo'n lange periode niet kunnen doorstaan zonder schadelijke veranderingen.

