Tiek uzskatīts, ka skaitļu jēdziens vispirms radās, kad aizvēsturiski cilvēki sāka lietot pirkstus, lai kaut ko skaitītu. Kopš tā laika cilvēce ir gājusi garu ceļu. Tagad mēs izmantojam kalkulatorus un datorus, lai saskaitītu lielākos skaitļus. Un pat nosaukumi ir parādījušies tik lieliem skaitļiem, ka tos diez vai var iedomāties.
Skaitāmo skaitļu bezgalība
Šķiet, ka atbilde uz jautājumu par to, kurš matemātikā ir vislielākais, ir ļoti vienkārša. Bezgalība, vai ne? Bet tas nav pilnīgi pareizi. Galu galā bezgalība nemaz nav skaitlis, bet gan jēdziens. Ideja.
Bezgalība (bezgalība) ir jēdziens, kas tulkojumā no latīņu valodas nozīmē "bez robežām". Bezgalības definīcija matemātikā saka, ka neatkarīgi no tā, cik liels ir skaitlis, jūs vienmēr varat tam pievienot 1, un tas kļūs lielāks.
Tāpēc, stingri sakot, nav tādas lietas kā lielākais skaits pasaulē. Jūs varat nosaukt tikai lielāko skaitli, kuram piešķirts konkrēts nosaukums.
Daži no slavenākajiem nosaukumiem lielam skaitam ir:
| Nulļu skaits | Nosaukums | Vārds angļu valodā |
|---|---|---|
| 3 | tūkstotis | tūkstotis |
| 6 | miljons | miljons |
| 9 | miljards (miljards) | miljards |
| 12 | triljons | triljons |
| 15 | kvadriljons | kvadriljons |
| 18 | kvintiljons | kvintiljons |
| 21 | sextillion | sextillion |
| 24 | septiljons | septiljons |
| 27 | astoņmiljons | astoņmiljons |
| 30 | kvintiljons | nonillion |
| 33 | decillion | decillion |
| 36 | undecillion | undecillion |
| 39 | duodecilions | duodecilions |
| 42 | tredeciljons | tredeciljons |
| 45 | quatuorddecillion | quattuordecillion |
| 48 | kvindeciljons | kvindeciljons |
| 51 | dzimšanas deciljons | dzimšanas deciljons |
| 54 | septendecilions | septendecilions |
| 57 | oktodeciljons | oktodeciljons |
| 60 | novemdecillion | novemdecillion |
| 63 | vigintiljons | vigintiljons |
| 66 | unvigintillion | unvigintillion |
| 69 | duovigintiljons | duovigintiljons |
| 72 | trevigintiljons | trevigintiljons |
| 75 | quatuorvigintillion | quattuorvigintillion |
| 78 | kvinvigintiljons | kvinvigintiljons |
| 81 | sexvigintillion | sexvigintillion |
| 84 | septenvigintillion | septenvigintillion |
| 87 | oktovigintiljons | oktovigintiljons |
| 90 | novemvigintillion | novemvigintillion |
| 93 | trigintiljons | trigintiljons |
| 96 | trigintiljons | trigintiljons |
| 99 | duotrigintillion | duotrigintillion |
| 102 | tretrigintiljons | trestrigintiljons |
| 105 | četrtrigintiljons | quattuortrigintillion |
| 108 | kvintrigintiljons | kvintrigintiljons |
| 111 | sextrigintillion | sextrigintillion |
| 114 | septentrigintiljons | septentrigintiljons |
| 117 | oktotrigintiljons | oktotrigintiljons |
| 120 | novemtrigintiljons | novemtrigintiljons |
| 123 | kvadragintiljons | kvadragintiljons |
| 126 | unquadragintillion | unquadragintillion |
| 129 | duetskadragintiljons | duokvadragintiljons |
| 132 | trackquadragintillion | trequadragintillion |
| 135 | quatorquadragintillion | quattuorquadragintillion |
| 138 | quinquadragintillion | quinquadragintillion |
| 141 | sexquadragintillion | sexquadragintillion |
| 144 | septinquadragintillion | septenquadragintillion |
| 147 | oktokvadragintiljons | oktokvadragintiljons |
| 150 | novemquadragintillion | novemquadragintillion |
| 153 | kvinkvintiljons | kvinkvintiljons |
| 156 | unquincagintillion | unquinquagintillion |
| 159 | duoquincagintillion | duquinquagintillion |
| 162 | trequincagintillion | trequinquagintillion |
| 165 | quatorquincagintillion | quattuorquinquagintillion |
| 168 | hinquincagintillion | hinquinquagintillion |
| 171 | sexquincagintillion | sexquinquagintillion |
| 174 | septenquincagintillion | septenquinquagintillion |
| 177 | oktokvinkagiljons | oktokvinquagintillion |
| 180 | novemquincagintillion | novemquinquagintillion |
| 183 | sexagintillion | sexagintillion |
| 186 | unsexagintillion | unsexagintillion |
| 189 | duosexagintillion | duosexagintillion |
| 192 | tresexagintillion | tresexagintillion |
| 195 | quatorsexagintillion | quattuorsexagintillion |
| 198 | quinsexagintillion | quinsexagintillion |
| 201 | sexsexagintillion | sexsexagintillion |
| 204 | septensexagintillion | septensexagintillion |
| 207 | oktosexagintillion | oktosexagintillion |
| 210 | novemsexagintillion | novemsexagintillion |
| 213 | septagintiljons | septuagintillion |
| 216 | nesagalvots | nepārdomāts |
| 219 | duoseptagintillion | duoseptuagintillion |
| 222 | treseptagintiljons | treseptuagintillion |
| 225 | kvatorseptagintiljons | quattuorseptuagintillion |
| 228 | kvinseptagintiljons | kvinseptuagintiljons |
| 231 | sexseptagintillion | sexseptuagintillion |
| 234 | septenseptagintiljons | septenseptuagintillion |
| 237 | oktoseptagintiljons | oktozeptuagintiljons |
| 240 | novemseptagintillion | novemseptuagintillion |
| 243 | oktogintiljons | oktogintiljons |
| 246 | unoctogintillion | unoctogintillion |
| 249 | duooktogintiljons | duooktogintiljons |
| 252 | tracktogintillion | treoktogintiljons |
| 255 | kvatoroktogintiljons | quattuoroctogintillion |
| 258 | kvinoktogintiljons | kvinoktogintiljons |
| 261 | sexoctogintillion | sexoctogintillion |
| 264 | septoktogintiljons | septoktogintiljons |
| 267 | oktoktogintiljons | oktoktogintiljons |
| 270 | novemoctogintillion | novemoctogintillion |
| 273 | nonagintillion | nonagintillion |
| 276 | neonagintiljons | neonagintiljons |
| 279 | duononagintillion | duononagintillion |
| 282 | trenonagintiljons | trenonagintiljons |
| 285 | quatornonagintillion | quattuornonagintillion |
| 288 | quinnonagintillion | quinnonagintillion |
| 291 | sexnagintillion | sexnonagintillion |
| 294 | septennonagintillion | septennonagintillion |
| 297 | oktononagintiljons | oktononagintiljons |
| 300 | novemnonagintillion | novemnonagintillion |
| 303 | simtmiljons | simtmiljons |
Kā sauc lielāko galveno skaitli
Galvenais skaitlis ir tāds, kas dalās tikai ar sevi un ar vienu. 2018. gada beigās amerikānis Patriks Laročs pasniedza zinātnes pasaulei vislielāko galveno skaitli.
- Tās garums ir 24 862 048 rakstzīmes. Salīdzinājumam: laikmetīgajā L.N. Tolstoja "Karš un miers" ir aptuveni 6-7 miljoni rakstzīmju, ja iekļaujat pieturzīmes un atstarpes.
- Šo numuru var rakstīt šādi: 282589933-1
- Un tas skan šādi: divi līdz 82589933 jaudai mīnus viens.
- Ir viss tiešsaistes projekts GIMPS, kura mērķis ir tieši atrast lielākos pirmizrādes. Tajā piedalās dažādu valstu matemātiķi. Tāpēc bieži parādās jauni ierakstu turētāji. Zinātnieki strādā, kā saka, nevis bailēs, bet gan naudas dēļ. Galu galā tas, kurš atver nākamo augstāko Mersenne prime, saņems 3000 USD.
Kāds ir lielākais skaits pasaulē
1980. gadā Ginesa rekordu grāmatā tika iekļauts Grehema numurs (tas ir arī G64 vai G), kas nosaukts amerikāņu matemātiķa Ronalda Grehema vārdā. Tas ir lielākais skaits, kāds jebkad izmantots svarīgā matemātiskā pierādījumā. Mēs runājam par Frenka Ramsija teoriju.
Īsumā par šo teoriju: iedomājieties N izmēru kubu, tā virsotnes nejauši savieno sarkanās vai zilās līnijas segmenti. Un mūsu uzdevums ir saprast, līdz kādai N vērtībai tas ir iespējams (ja dažādos veidos krāsojam pāri kuba malām), lai izvairītos no situācijas, kad viena kuba plakne tiks nokrāsota ar vienu krāsu. Tas ir, mums nevajadzētu iegūt vienkrāsainu "aploksni".
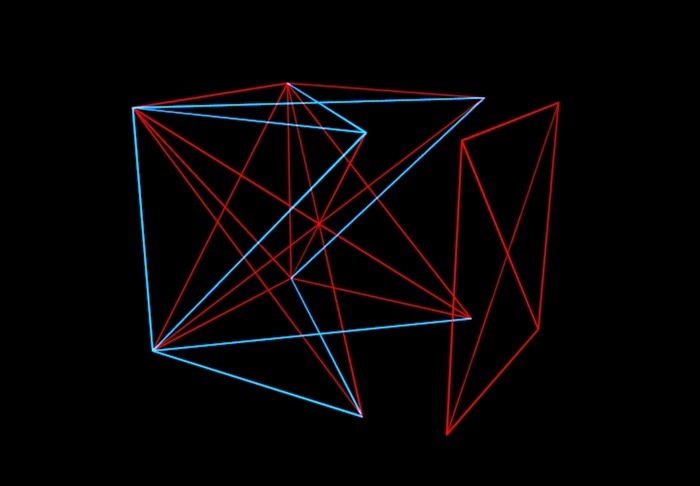
Matemātiķi šādā veidā nokrāsoja kubu un izrādījās, ka līdz sešdimensiju kubam jūs varat izdomāt un panākt, ka vienas krāsas līnijas, kas savieno četras virsotnes, neatrodas vienā plaknē. Bet ar septiņdimensiju, kā uzzināja Greiems un Rotšilds, šāds triks vairs nav iespējams. Un ar astoņdimensiju. Un ... "un tā tālāk", kas tomēr nav bezgalīgs, bet beidzas ar fantastiski gigantisku skaitli. To viņi sauc par Greiema numuru. Starp citu, Greiema un Rotšildu risinājums tagad ir novecojis. Matemātiķi ir noskaidrojuši, ka 6-7-8-9-10-11-12 dimensiju kubus joprojām var krāsot bez aploksnēm. Bet kaut kur starp 13 un Greiema numuru garantēti ir skaitlis, virs kura jebkurā gadījumā būs "aploksnes".
Grehema numurs ieguva pasaules mēroga atpazīstamību 1977. gadā, kad slavenais zinātnes popularizētājs Martins Gārdners par to rakstīja žurnālā Scientific American.
Un, lai gan kopš tā laika matemātikā ir bijuši citi kandidāti uz vislielākā skaita titulu, Grehema "ideju radīšana" ir vispopulārākā un zināmākā. Un, ja esat dzirdējuši par "ogļu ģimeni":
- googol - 10100;
Vai: 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 - googolplex - 10googol,
tad jums vajadzētu zināt, ka šie skaitļi matemātikā ir tikai "mīcīšana", un Greiema skaitlis ir neiedomājams reižu lielāks skaitlis nekā viņi. Un pat vairāk nekā Skuse skaitlis starp 1019 un 1.3971672 10316 un aptuveni vienāds e727,951336108.
Interesanti, ka, izgudrojot googol, amerikāņu matemātiķis Edvards Kazners vēlējās studentiem parādīt atšķirību starp neticami lielu skaitu un bezgalību. Tad Greiema skaitlis varētu vienkārši "izpūst prātu".
Vai ir iespējams iedomāties un pierakstīt skaitli, kas nav saprotams?
Matemātiķi nevarēs pateikt precīzu ciparu skaitu Greiema skaitā, nemaz nerunājot par viņu skaitīšanu. Ir zināmi tikai pēdējie 50 cipari no lielākā skaita pasaulē - tas ir ... 0322234872396701848518643905910457562726246464195387.
Bet skaitļi, ar kuriem sākas G64, nav zināmi un diez vai kādreiz būs.
Salīdzināsim trīs monstrus: googol, googolplex un Grehema numuru.
- Googol ir Visumā ietilpīgo smilšu graudu skaits, kas reizināts ar 10 miljardiem.Tātad, iedomājieties Visumu, kas piepildīts ar maziem smilšu graudiņiem - desmitiem miljardu gaismas gadu virs Zemes, zem tās, tās priekšā, aiz tās - bezgalīgas smiltis.
Tagad iedomājieties, ka kādā brīdī jūs paņemat vienu smilšu graudu, lai to pārbaudītu spēcīgā mikroskopā. Un jūs redzat, ka patiesībā tas nav vienīgais grauds, bet gan 10 miljardi mikroskopisko graudu, un kopā tie ir smilšu graudu lielumā. Ja tas būtu gadījumā ar katru atsevišķo smilšu graudu šajā hipotētiskajā Visumā, tad šo mikroskopisko graudu kopsumma būtu googols.
- Lai noteiktu googolplex, astronoms un astrofiziķis Karls Sagans sniedza piemēru, kā visu novērojamā Visuma tilpumu piepilda ar aptuveni 1,5 mikrometru lielām smalkām putekļu daļiņām. Pamatojoties uz to, dažādu kombināciju, kurās šīs daļiņas var atrasties, kopējais skaits būs aptuveni vienāds ar vienu googolplex.
- Tagad iedomājieties, ka googolplex nav pat smilšu grauds, bet gan niecīgs punkts, kuru var redzēt tikai caur visspēcīgāko mikroskopu. Un viss mūsu Visums ir piepildīts ar tik niecīgiem punktiem. Tātad, pat tas nav salīdzināms ar Greiema skaitli. Bet ko tad, ja mēs vēlamies izmantot visu novērojamā Visuma telpu, lai to ierakstītu (pieņemsim, ka katra cipara ierakstīšana aizņem vismaz Planck apjomu)? Ak, tas mums nederēs! Bet jūs vienmēr varat iet citu ceļu.
Kā rakstīt G64, izmantojot Knuta metodi
1976. gadā amerikāņu zinātnieks Donalds Knuts ierosināja supergrādu jeb Knuta apzīmējumu koncepciju. Šī ir metode, kas ļauj rakstīt ļoti lielus skaitļus, izmantojot augšupvērstās bultiņas. Eksponenci apzīmē ar vienu bultiņu uz augšu: ↑.
Šādi izskatās šis apzīmējums: a ↑ b = ab = a × a × a ×… un tā tālāk b reizes.
- Piemēram, 3 ↑ 3 = 3³.
- Googol ir rakstīts kā 10 ↑ 10 ↑ 2.
- Googolplex - 10 ↑ 10 ↑ 10 ↑ 2
Svarīga augšupvērsto bultiņu iezīme ir tā, ka tās aug ļoti ātri. Ekspozīcija aug daudz ātrāk nekā reizināšana. 2 × 10 ir tikai 20, bet 2 ↑ 10 = 1024. Tādā pašā veidā katrs jauns bultiņu līmenis aug daudz ātrāk nekā iepriekšējais.
Ja jūs garīgi iztēlojaties trīsvietīgu spēka torni 3 ↑↑↑ 4, jūs saņemsiet struktūru, kuras lielums svārstās no Zemes līdz Marsam. Bet mēs pat neesam sasnieguši “apakšējo pakāpienu”, kas mūs noved pie Greiema skaita.
Mēs varam aprakstīt Grehema numuru ar milzīgu šo augšupvērsto bultiņu kopu.
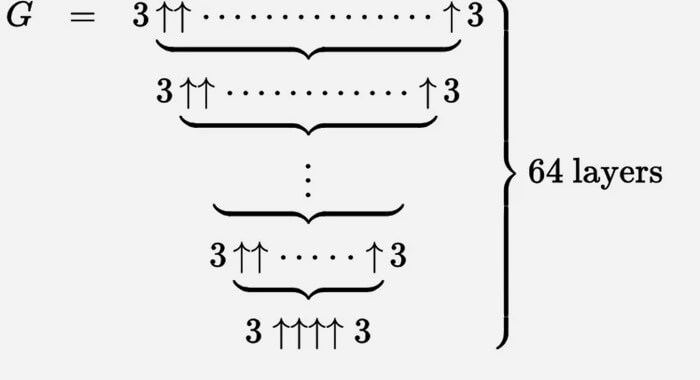
Visvieglāk to domāt par iteratīvu procesu. Mēs sākam no apakšas ar g 1 = 3 ↑↑↑↑ 3 un pēc tam izveidojam otro rindu (sauksim to par g 2) ar bultiņām g 1 starp trīskāršiem.
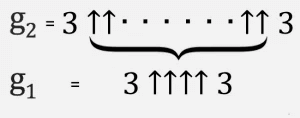
Tad g 3 ir divi trīskārši, atdalīti ar g 2 augšupvērstām bultiņām utt., Līdz g 64 ar g 63 bultiņām starp trīskāršiem ir Greiema skaitlis.
Ja nemirstības vietā izvēlaties dzīves ilgumu, kas vienāds ar Greiema skaitli, rezultāts būs gandrīz tāds pats. Pat ja pieņemam, ka apstākļi Visumā, Saules sistēmā un uz Zemes uz visiem laikiem paliks nemainīgi, cilvēka smadzenes, iespējams, nebūtu varējušas izturēt tik ilgu laika periodu bez kaitīgām izmaiņām.