Manoma, kad skaičių sąvoka pirmą kartą atsirado tada, kai priešistoriniai žmonės pradėjo pirštais kažką skaičiuoti. Nuo to laiko žmonija nuėjo ilgą kelią. Dabar skaičiuoklėms ir kompiuteriams naudojame daugiausiai skaičių. Ir netgi atsirado skaičių, kurie yra tokie dideli, kad jų beveik neįmanoma įsivaizduoti.
Begalybė skaičiuojamų skaičių
Atrodytų, kad atsakymas į klausimą, koks yra didžiausias matematikos skaičius, yra labai paprastas. Begalybė, tiesa? Bet tai nėra visiškai teisinga. Juk begalybė yra visai ne skaičius, o sąvoka. Idėja.
Begalybė (infinitum) yra sąvoka, kuri išvertus iš lotynų kalbos reiškia „be sienų“. Begalybės apibrėžimas matematikoje sako, kad nesvarbu, koks didelis skaičius, bet visada galite jį pridėti 1 ir jis padidės.
Todėl griežtai kalbant, nėra tokio dalyko kaip didžiausias skaičius pasaulyje. Galite įvardyti tik didžiausią skaičių, suteiktą konkrečiam pavadinimui.
Kai kurie labiau žinomi didelių skaičių pavadinimai yra šie:
| Nulių skaičius | vardas | Pavadinimas angliškai |
|---|---|---|
| 3 | tūkstantis | tūkstantis |
| 6 | mln | mln |
| 9 | milijardas (milijardas) | mlrd |
| 12 | trilijoną | trilijoną |
| 15 | kvadrilijonas | kvadrilijonas |
| 18 | kvintilijonas | kvintilijonas |
| 21 | sekstilijonas | sekstilijonas |
| 24 | septilija | septilija |
| 27 | aštuoniasdešimt | aštuoniasdešimt |
| 30 | kvintilijonas | nonillion |
| 33 | decillion | decillion |
| 36 | undecillion | undecillion |
| 39 | dvylikapirštės žarnos | dvylikapirštės žarnos |
| 42 | trececilijonas | trececilijonas |
| 45 | quatuorddecillion | quattuordecillion |
| 48 | kvindecilijonas | kvindecilijonas |
| 51 | sexdecillion | sexdecillion |
| 54 | septendecilijonas | septendecilijonas |
| 57 | aštuonkampis | aštuonkampis |
| 60 | novemdecilijonas | novemdecilijonas |
| 63 | budėjimas | budėjimas |
| 66 | nepakeliamas | nepakeliamas |
| 69 | duovigintilijonas | duovigintilijonas |
| 72 | trevigintilijonas | trevigintilijonas |
| 75 | quatuorvigintillion | quattuorvigintillion |
| 78 | kvinvigintilijonas | kvinvigintilijonas |
| 81 | sexvigintillion | sexvigintillion |
| 84 | septenvigintilijonas | septenvigintilijonas |
| 87 | oktovigintilijonas | oktovigintilijonas |
| 90 | novemvigintilijonas | novemvigintilijonas |
| 93 | trigintilijonas | trigintilijonas |
| 96 | netrintilijonas | netrintilijonas |
| 99 | duotrigintilijonas | duotrigintilijonas |
| 102 | tretrigintilijonas | trestrigintilijonas |
| 105 | keturi trigintilijonai | quattuortrigintillion |
| 108 | kvintrigintilijonas | kvintrigintilijonas |
| 111 | sextrigintillion | sextrigintillion |
| 114 | septentrigintilijonas | septentrigintilijonas |
| 117 | oktotrigintilijonas | oktotrigintilijonas |
| 120 | novemtrigintilijonas | novemtrigintilijonas |
| 123 | keturkampis | keturkampis |
| 126 | unquadragintillion | unquadragintillion |
| 129 | duekvadragintilijonas | duekvadragintilijonas |
| 132 | takelio kvadrilijonas | trequadragintillion |
| 135 | quatorquadragintillion | quattuorquadragintillion |
| 138 | quinquadragintillion | quinquadragintillion |
| 141 | sexquadragintillion | sexquadragintillion |
| 144 | septinkvadragintilijonas | septenquadragintillion |
| 147 | oktokvadragintilijonas | oktokvadragintilijonas |
| 150 | novemquadragintillion | novemquadragintillion |
| 153 | penkiakvintilijonas | penkiakvintilijonas |
| 156 | nekankintinis | nekvinikagilijonas |
| 159 | duekinkagilijonas | duquinquagintillion |
| 162 | trequincagintillion | trequinquagintillion |
| 165 | quatorquincagintillion | quattuorquinquagintillion |
| 168 | chinquincagintillion | chinquinquagintillion |
| 171 | sexquinkagintillion | sexquinquagintillion |
| 174 | septenquincagintillion | septenquinquagintillion |
| 177 | oktokvinkagilijonas | oktokvinquagintilijonas |
| 180 | novemquincagintillion | novemquinquagintillion |
| 183 | sexagintillion | sexagintillion |
| 186 | neseksagintilijonas | neseksagintilijonas |
| 189 | duosexagintillion | duosexagintillion |
| 192 | tresexagintillion | tresexagintillion |
| 195 | kvatoraksagilijonas | quattuorsexagintillion |
| 198 | quinsexagintillion | quinsexagintillion |
| 201 | sexsexagintillion | sexsexagintillion |
| 204 | septensexagintillion | septensexagintillion |
| 207 | oktosexagintillion | oktosexagintillion |
| 210 | novemsexagintillion | novemsexagintillion |
| 213 | septagintilijonas | septintagintilijonas |
| 216 | nepagalvotas | nepagalvotas |
| 219 | duoseptagintilijonas | duoseptuagintillion |
| 222 | treseptagintilijonas | treseptuagintillion |
| 225 | quatorseptagintillion | quattuorseptuagintillion |
| 228 | kvinseptagintilijonas | kvinseptuagintilijonas |
| 231 | sexseptagintillion | sexseptuagintillion |
| 234 | septenseptagintilijonas | septenseptuagintilijonas |
| 237 | oktoseptagintilijonas | oktoseptuagintilijonas |
| 240 | novemseptagintillion | novemseptuagintillion |
| 243 | oktogintilijonas | oktogintilijonas |
| 246 | unoctogintillion | unoctogintillion |
| 249 | duooktogintilijonas | duooktogintilijonas |
| 252 | tracktogintillion | treoktogintilijonas |
| 255 | kvatoroktogintilijonas | quattuoroctogintillion |
| 258 | kvinoktogintilijonas | kvinoktogintilijonas |
| 261 | sexoctogintillion | sexoctogintillion |
| 264 | septoktogintilijonas | septoktogintilijonas |
| 267 | oktoktogintilijonas | oktoktogintilijonas |
| 270 | novemoctogintillion | novemoctogintillion |
| 273 | nonagintillion | nonagintillion |
| 276 | neįtikėtinas | neįtikėtinas |
| 279 | duononagintilijonas | duononagintilijonas |
| 282 | trenonagintilijonas | trenonagintilijonas |
| 285 | quatornonagintillion | quattuornonagintillion |
| 288 | quinnonagintillion | quinnonagintillion |
| 291 | sexnagintillion | sexnonagintillion |
| 294 | septennonagintillion | septennonagintillion |
| 297 | oktononagintilijonas | oktononagintilijonas |
| 300 | novemnonagintillion | novemnonagintillion |
| 303 | šimto milijonų | šimto milijonų |
Koks yra didžiausio pirminio skaičiaus pavadinimas
 Pirminis skaičius yra tas, kuris dalijasi tik pats iš savęs ir iš vieno. 2018 metų pabaigoje amerikietis Patrickas Laroche'as mokslo pasauliui pristatė didžiausią skaičių.
Pirminis skaičius yra tas, kuris dalijasi tik pats iš savęs ir iš vieno. 2018 metų pabaigoje amerikietis Patrickas Laroche'as mokslo pasauliui pristatė didžiausią skaičių.
- Jo ilgis yra 24 862 048 simboliai. Palyginimui: epochiniame kūrinyje L.N. Tolstojaus „Karas ir taika“ yra apie 6–7 milijonus simbolių, jei įtraukiate skyrybos ženklus ir tarpus.
- Šį skaičių galima parašyti taip: 282589933-1
- Ir jis rašo taip: du - 82589933 galia, atėmus vieną.
- Yra visas internetinis projektas GIMPS, kurio tikslas yra rasti didžiausius pradmenis. Jame dalyvauja matematikai iš įvairių šalių. Todėl nauji rekordininkai dažnai pasirodo. Mokslininkai dirba, kaip sakoma, ne dėl baimės, o dėl pinigų. Galų gale, kas atidarys kitą didžiausią „Mersenne Prime“, gaus 3000 USD.
Koks yra didžiausias skaičius pasaulyje
 1980 m. Į Gineso rekordų knygą buvo įtrauktas „Graham“ numeris (tai taip pat G64 arba G), pavadintas amerikiečių matematiko Ronaldo Grahamo vardu. Tai didžiausias skaičius, kada nors panaudotas svarbiam matematiniam įrodymui. Mes kalbame apie Franko Ramsey teoriją.
1980 m. Į Gineso rekordų knygą buvo įtrauktas „Graham“ numeris (tai taip pat G64 arba G), pavadintas amerikiečių matematiko Ronaldo Grahamo vardu. Tai didžiausias skaičius, kada nors panaudotas svarbiam matematiniam įrodymui. Mes kalbame apie Franko Ramsey teoriją.
Trumpai apie šią teoriją: įsivaizduokite N matmenų kubą, kurio viršūnės yra atsitiktinai sujungtos raudonos arba mėlynos linijos atkarpomis. Ir mūsų užduotis yra suprasti, iki kokios N vertės galima (jei kubo kraštai dažomi skirtingais būdais), išvengti situacijos, kai viena kubo plokštuma bus nudažyta viena spalva. Tai yra, neturėtume gauti vienspalvio „voko“.
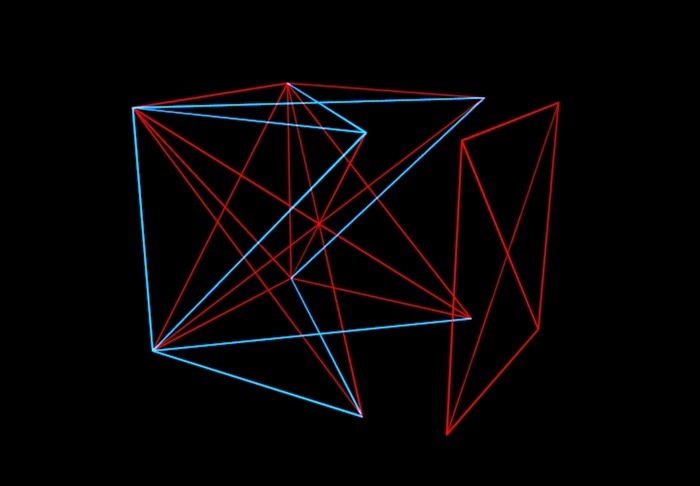
Matematikai nupiešė kubą taip ir taip. Paaiškėjo, kad iki šešių dimensijų kubo galite sumanyti ir priversti tos pačios spalvos linijas, jungiančias keturias viršūnes, negulėti vienoje plokštumoje. Tačiau turint septynių dimensijų, kaip sužinojo Grahamas ir Rothschildas, toks triukas nebegalimas. Ir su aštuoniais matmenimis. Ir ... „ir taip toliau“, kuris vis dėlto nėra begalinis, bet baigiasi fantastiškai gigantišku skaičiumi. Tai jie vadina Greimo numeriu. Beje, Grahamo ir Rothschildo sprendimas dabar yra pasenęs. Matematikai išsiaiškino, kad 6-7-8-9-10-11-12 matmenų kubus vis tiek galima dažyti be vokų. Bet kažkur tarp 13 ir Greimo numerio garantuotai bus skaičius, virš kurio bet kuriuo atveju bus „vokai“.
Grahamo skaičius sulaukė pasaulinio pripažinimo 1977 m., Kai garsus mokslo populiarintojas Martinas Gardneris apie tai parašė „Scientific American“.
Ir nors nuo to laiko buvo ir kitų kandidatų į daugiausiai matematikos titulą, populiariausias ir žinomiausias yra Grahamo „idėjos“. O jei girdėjote apie „anglių šeimą“:
- „googol“ - 10100;
Arba: 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 - „googolplex“ - 10googol,
tada turėtumėte žinoti, kad šie matematikos skaičiai yra tik „minkyti“, o Grahamo skaičius yra neįsivaizduojamas skaičius kartų didesnis už juos. Ir net daugiau nei „Skuse“ skaičius tarp 1019 ir 1.3971672 10316 ir maždaug vienodi e727,951336108.
Įdomu tai, kad išradęs „googol“ amerikiečių matematikas Edwardas Kazneris norėjo parodyti studentams skirtumą tarp neįtikėtinai didelio skaičiaus ir begalybės. Tada Grahamo skaičius gali tiesiog „papūsti galvą“.
Ar įmanoma įsivaizduoti ir užrašyti nesuprantamą skaičių?
Matematikai negalės pasakyti tikslaus skaičių skaičių pagal Grahamo skaičių, o ką jau kalbėti apie jo skaičiavimą. Žinomi tik paskutiniai 50 skaitmenų iš didžiausio skaičiaus pasaulyje - tai yra ... 03222348723967018485186439059104575627262464195387.
Tačiau skaičiai, nuo kurių prasideda G64, nėra žinomi ir vargu ar kada nors bus.
Palyginkime tris monstrus: googol, googolplex ir Graham numerį.
- „GoogleGol“ - tai visatoje tinkamų smėlio grūdelių skaičius, padaugintas iš 10 milijardų.Taigi, įsivaizduokite visatą, užpildytą mažais smėlio grūdeliais - dešimtimis milijardų šviesmečių virš Žemės, po ja, priešais ją, už jos - begalinis smėlis.
Dabar įsivaizduokite, kad tam tikru momentu paimate vieną smėlio grūdelį, kad galėtumėte jį ištirti galingu mikroskopu. Ir matote, kad iš tikrųjų tai yra ne vienas grūdas, o 10 milijardų mikroskopinių grūdelių, o kartu jie yra smėlio grūdelio dydžio. Jei taip būtų kiekviename smėlio grūdelyje šioje hipotetinėje visatoje, tai šių mikroskopinių grūdų suma būtų googolis.
- Norėdamas kiekybiškai įvertinti „googolplex“, astronomas ir astrofizikas Carlas Saganas pateikė pavyzdį, kaip visas stebimos visatos tūris buvo užpildytas maždaug 1,5 mikrometro dydžio smulkių dulkių dalelėmis. Remiantis tuo, bendras skirtingų derinių, kuriuose gali būti šios dalelės, skaičius bus maždaug lygus vienam googolplex.
- Dabar įsivaizduokime, kad „googolplex“ nėra net smėlio grūdelis, o mažytis taškelis, į kurį galima žiūrėti tik per galingiausią mikroskopą. Ir visa mūsų visata yra užpildyta tokiais mažais taškeliais. Taigi, net tai nėra galima palyginti su Greimo skaičiumi. Bet ką daryti, jei norime panaudoti visą stebimos visatos erdvę jai įrašyti (tarkime, kad kiekvieno skaitmens įrašymas užima bent Plancko tūrį)? Deja, mums tai netiks! Bet visada galite eiti kitu keliu.
Kaip parašyti G64 naudojant Knuth metodą
1976 m. Amerikiečių mokslininkas Donaldas Knuthas pasiūlė superastrų koncepciją arba Knutho žymėjimą. Tai metodas, leidžiantis rašyti labai didelius skaičius naudojant rodykles aukštyn. Pailginimas žymimas viena rodykle aukštyn: ↑.
Taip atrodo šis žymėjimas: a ↑ b = ab = a × a × a ×… ir taip toliau b kartus.
- Pavyzdžiui, 3 ↑ 3 = 3³.
- „Google“ yra parašyta 10 × 10 × 2.
- „Googolplex“ - 10 ↑ 10 ↑ 10 ↑ 2
Svarbi rodyklių aukštyn ypatybė yra ta, kad jos auga labai greitai. Ekspozicija auga daug greičiau nei dauginimas. 2 × 10 yra tik 20, bet 2 ↑ 10 = 1024. Lygiai taip pat kiekvienas naujas rodyklių lygis auga daug greičiau nei ankstesnis.
Jei mintyse įsivaizduosite 3 ↑↑↑ 4 tripletų galios bokštą, gausite struktūrą, kurios dydis svyruoja nuo Žemės iki Marso. Bet mes net nepasiekėme „apatinio laiptelio“, kuris mus atveda prie Greimo numerio.
Greimo skaičių galime apibūdinti didžiuliu šių rodyklių į viršų rinkiniu.
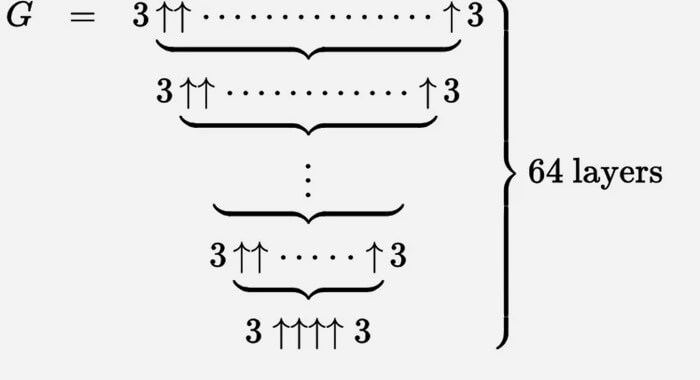
Lengviausia tai laikyti iteraciniu procesu. Pradedame nuo apačios su g 1 = 3 ↑↑↑↑ 3, tada sukuriame antrą eilutę (pavadinkime ją g 2) su rodyklėmis g 1 tarp tripletų.
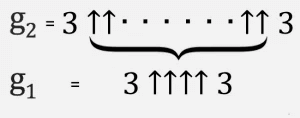
Tada g 3 yra du trigubai, atskirti g 2 rodyklėmis į viršų ir pan., Kol g 64 su g 63 rodyklėmis tarp trigubų yra Graham skaičius.
Jei vietoj nemirtingumo pasirinksite gyvenimo trukmę, lygią „Graham“ skaičiui, rezultatas bus beveik toks pats. Net jei manytume, kad sąlygos Visatoje, Saulės sistemoje ir Žemėje amžinai išliks nepakitusios, žmogaus smegenys negalėjo ištverti tokio ilgo laikotarpio be žalingų pokyčių.

