Úgy gondolják, hogy a számok fogalma először akkor keletkezett, amikor az őskori emberek ujjaikkal kezdtek számolni valamit. Azóta az emberiség hosszú utat tett meg. Most számológépekkel és számítógépekkel számoljuk a legnagyobb számokat. És még olyan nevek is megjelentek, amelyek akkora számok, hogy alig lehet elképzelni őket.
Megszámlálható számok végtelensége
Úgy tűnik, hogy a kérdésre, hogy mi a legnagyobb szám a matematikában, nagyon egyszerű a válasz. Végtelen, igaz? De ez nem teljesen helyes. Végül is a végtelenség egyáltalán nem szám, hanem fogalom. Ötlet.
A végtelen (infinitum) egy olyan fogalom, amely a latin fordításban "határok nélkül" jelent. A matematika végtelen definíciója szerint bármennyire is nagy egy szám, mindig adhat hozzá 1-et, és nagyobb lesz.
Ezért szigorúan véve nem létezik a világon a legnagyobb szám. Csak azt a legnagyobb számot lehet megnevezni, amely adott nevet kapott.
Néhány nagyszámú híresebb név:
| Nullák száma | Név | Név angolul |
|---|---|---|
| 3 | ezer | ezer |
| 6 | millió | millió |
| 9 | milliárd (milliárd) | milliárd, ezermillió |
| 12 | billió | billió |
| 15 | kvadrillió | kvadrillió |
| 18 | ötmilliárd | ötmilliárd |
| 21 | sextillion | sextillion |
| 24 | septillion | septillion |
| 27 | nyolcmilliárd | nyolcmilliárd |
| 30 | ötmilliárd | nonillion |
| 33 | decillion | decillion |
| 36 | undecillion | undecillion |
| 39 | duodecillion | duodecillion |
| 42 | trececillió | trececillió |
| 45 | quatuorddecillion | quattuordecillion |
| 48 | quindecillion | quindecillion |
| 51 | sexdecillion | sexdecillion |
| 54 | septendillió | septendillió |
| 57 | oktodecillió | oktodecillió |
| 60 | novemdecillion | novemdecillion |
| 63 | vigintillion | vigintillion |
| 66 | nem vigintillion | unvintillion |
| 69 | duovigintillion | duovigintillion |
| 72 | trevigintillion | trevigintillion |
| 75 | quatuorvigintillion | quattuorvigintillion |
| 78 | quinvigintillion | quinvigintillion |
| 81 | sexvigintillion | sexvigintillion |
| 84 | septenvigintillion | septenvigintillion |
| 87 | oktovigintillió | oktovigintillió |
| 90 | novemvigintillion | novemvigintillion |
| 93 | trigintillió | trigintillió |
| 96 | untrigintillion | untrigintillion |
| 99 | duotrigintillion | duotrigintillion |
| 102 | tretrigintillió | trestrigintillion |
| 105 | quattrigintillion | quattuortrigintillion |
| 108 | kvintrigintillió | kvintrigintillió |
| 111 | sextrigintillion | sextrigintillion |
| 114 | septentrigintillion | septentrigintillion |
| 117 | oktotrigintillió | oktotrigintillió |
| 120 | novemtrigintillion | novemtrigintillion |
| 123 | quadragintillion | quadragintillion |
| 126 | unquadragintillion | unquadragintillion |
| 129 | duóquadragintillion | duóquadragintillion |
| 132 | trackquadragintillion | trequadragintillion |
| 135 | quatorquadragintillion | quattuorquadragintillion |
| 138 | quinquadragintillion | quinquadragintillion |
| 141 | sexquadragintillion | sexquadragintillion |
| 144 | septinquadragintillion | septenquadragintillion |
| 147 | oktokvadragintillió | oktokvadragintillió |
| 150 | novemquadragintillion | novemquadragintillion |
| 153 | quinquagintillion | quinquagintillion |
| 156 | unquincagintillion | quinquagintillion |
| 159 | duoquincagintillion | duoquinquagintillion |
| 162 | trequincagintillion | trequinquagintillion |
| 165 | quatorquincagintillion | quattuorquinquagintillion |
| 168 | quinquincagintillion | quinquinquagintillion |
| 171 | sexquincagintillion | sexquinquagintillion |
| 174 | septenquincagintillion | septenquinquagintillion |
| 177 | octoquincagintillion | oktokvinquagintillion |
| 180 | novemquincagintillion | novemquinquagintillion |
| 183 | sexagintillion | sexagintillion |
| 186 | unsexagintillion | unsexagintillion |
| 189 | duosexagintillion | duosexagintillion |
| 192 | tresexagintillion | tresexagintillion |
| 195 | quatorsexagintillion | quattuorsexagintillion |
| 198 | quinsexagintillion | quinsexagintillion |
| 201 | sexsexagintillion | sexsexagintillion |
| 204 | septensexagintillion | septensexagintillion |
| 207 | octosexagintillion | octosexagintillion |
| 210 | novemsexagintillion | novemsexagintillion |
| 213 | septagintillion | septuagintillion |
| 216 | elképzelhetetlen | elképzelhetetlen |
| 219 | duoseptagintillion | duoseptuagintillion |
| 222 | treseptagintillion | treseptuagintillion |
| 225 | quatorseptagintillion | quattuorseptuagintillion |
| 228 | quinseptagintillion | quinseptuagintillion |
| 231 | sexseptagintillion | sexseptuagintillion |
| 234 | septenseptagintillion | septenseptuagintillion |
| 237 | octoseptagintillion | octoseptuagintillion |
| 240 | novemseptagintillion | novemseptuagintillion |
| 243 | octogintillion | octogintillion |
| 246 | unoctogintillion | unoctogintillion |
| 249 | duooctogintillion | duooctogintillion |
| 252 | tracktogintillion | treoctogintillion |
| 255 | quatoroctogintillion | quattuoroctogintillion |
| 258 | quinoctogintillion | quinoctogintillion |
| 261 | sexoctogintillion | sexoctogintillion |
| 264 | septoktogintillion | septoctogintillion |
| 267 | oktoktogintillió | oktoktogintillió |
| 270 | novemoctogintillion | novemoctogintillion |
| 273 | nonagillill | nonagillill |
| 276 | nononagintillion | nononagintillion |
| 279 | duononagintillion | duononagintillion |
| 282 | trenonagintillion | trenonagintillion |
| 285 | quatornonagintillion | quattuornonagintillion |
| 288 | quinnonagintillion | quinnonagintillion |
| 291 | sexnagintillion | sexnonagintillion |
| 294 | septennonagintillion | septennonagintillion |
| 297 | octononagintillion | octononagintillion |
| 300 | novemnonagintillion | novemnonagintillion |
| 303 | százmillió | százmillió |
Mi a legnagyobb prímszám neve
 A prímszám az, amely csak önmagában és egyenként osztható meg. 2018 végén az amerikai Patrick Laroche mutatta be a legnagyobb prímszámot a tudományos világ számára.
A prímszám az, amely csak önmagában és egyenként osztható meg. 2018 végén az amerikai Patrick Laroche mutatta be a legnagyobb prímszámot a tudományos világ számára.
- Hossza 24 862 048 karakter. Összehasonlításképpen: L.N. korszakalkotó munkájában. Tolsztoj "Háború és béke" körülbelül 6-7 millió karakter, ha az írásjeleket és a szóközöket is beleszámítjuk.
- Ez a szám a következõképpen írható: 282589933-1
- És ez így hangzik: kettő a 82589933 erejéig mínusz egy.
- Van egy egész online GIMPS projekt, amelynek célja pontosan a legnagyobb prímek megtalálása. Különböző országok matematikusai vesznek részt benne. Ezért gyakran jelennek meg új rekordtulajdonosok. A tudósok, mint mondják, nem a félelemért, hanem a pénzért dolgoznak. Végül is, aki megnyitja a következő legmagasabb Mersenne prime-ot, 3000 dollárt kap.
Mi a legnagyobb szám a világon
 1980-ban a Guinness-rekordok könyve tartalmazta a Graham számot (ez szintén G64 vagy G), amelyet Ronald Graham amerikai matematikusról neveztek el. Ez az eddigi legnagyobb szám egy fontos matematikai bizonyításban. Frank Ramsey elméletéről beszélünk.
1980-ban a Guinness-rekordok könyve tartalmazta a Graham számot (ez szintén G64 vagy G), amelyet Ronald Graham amerikai matematikusról neveztek el. Ez az eddigi legnagyobb szám egy fontos matematikai bizonyításban. Frank Ramsey elméletéről beszélünk.
Röviden erről az elméletről: képzeljünk el egy N-dimenziós kockát, amelynek csúcsait véletlenszerűen összekapcsolják piros vagy kék vonalszakaszok. Feladatunk pedig annak megértése, hogy milyen N értékig lehetséges (ha különböző módon festjük át a kocka széleit), hogy elkerüljük azt a helyzetet, amikor a kocka egy síkját egy színnel festjük. Vagyis nem szabad egyszínű "borítékot" kapnunk.
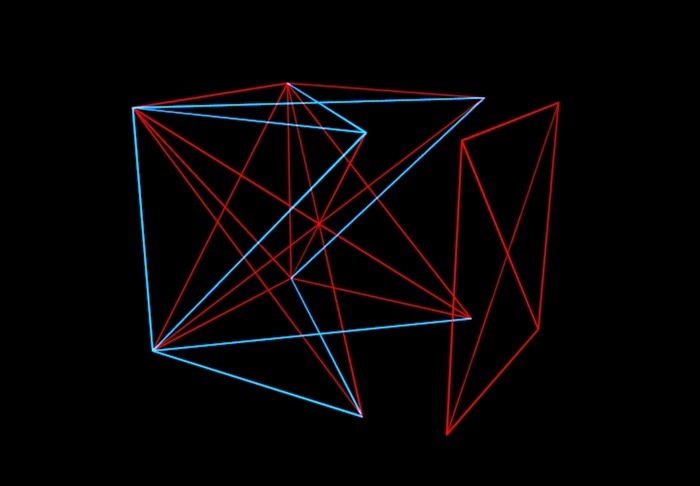
A matematikusok így és úgy festették a kockát, kiderült, hogy egy hatdimenziós kocka erejéig lehet fogantatni, és a négy csúcsot összekötő azonos színű vonalak nem fekszenek egy síkban. De a hétdimenziósokkal, mint Graham és Rothschild megtudták, ilyen trükk már nem lehetséges. És nyolcdimenzióssal. És ... "és így tovább", ami azonban nem végtelen, de egy fantasztikusan gigantikus számmal végződik. Ezt hívják Graham számának. Egyébként Graham és Rothschild megoldása mára elavult. Matematikusok rájöttek, hogy 6-7-8-9-10-11-12 dimenziós kockák továbbra is borítékok nélkül festhetők. De valahol 13 és Graham száma között garantáltan van olyan szám, amely felett mindenképpen "borítékok" lesznek.
Graham száma 1977-ben világszerte elismert, amikor a tudomány híres népszerűsítője, Martin Gardner írt róla a Scientific American-ben.
És bár azóta vannak más jelöltek is a matematika legnagyobb számának címére, Graham "agyszüleménye" a legnépszerűbb és legismertebb. És ha hallottál a "széncsaládról":
- googol - 10100;
Vagy: 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 - googolplex - 10googol,
akkor tudnia kell, hogy ezek a számok a matematikában csak "gyúrnak", és Graham száma elképzelhetetlen számú, nagyobb, mint ők. És még több is, mint egy 10 közötti Skuse-szám19 és 1.3971672 10316 és megközelítőleg egyenlő e727,951336108.
Érdekesség, hogy a googol feltalálásával Edward Kazner amerikai matematikus meg akarta mutatni a hallgatóknak a hihetetlenül nagy szám és a végtelen közötti különbséget. Aztán Graham száma csak "kifújhatja a fejét".
El lehet-e képzelni és felfogni egy számot, amelyen érthetetlen?
A matematikusok nem fogják tudni megmondani a számjegyek pontos számát Graham számában, nemhogy számolni vele. Csak a világ legnagyobb számának utolsó 50 számjegye ismert - ez ... 03222348723967018485186439059104575627262464195387.
De a számok, amelyekkel a G64 kezdődik, ismeretlenek, és aligha lesznek soha.
Hasonlítsunk össze három szörnyet: googol, googolplex és Graham számát.
- A Googol az univerzumban elférő homokszemek száma, megszorozva 10 milliárddal.Tehát képzeljen el egy univerzumot, amely tele van apró homokszemekkel - több tízmilliárd fényévvel a Föld felett, alatta, előtte, mögötte - végtelen homokkal.
Most képzelje el, hogy valamikor vesz egy szem homokot, hogy erős mikroszkóp alatt megvizsgálja. És látja, hogy valójában nem ez az egyetlen szemcse, hanem 10 milliárd mikroszkopikus szem, és ezek együttesen akkorák, mint egy homokszem. Ha ez a helyzet minden egyes homokszem esetében ebben a hipotetikus univerzumban, akkor ezeknek a mikroszkopikus szemcséknek az összege googol lenne.
- A googolplex számszerűsítéséhez Carl Sagan csillagász és asztrofizikus példát hozott arra, hogy a megfigyelhető univerzum teljes térfogatát kb. 1,5 mikrométer nagyságú finom porszemcsékkel töltötték meg. Ennek alapján a különféle kombinációk száma, amelyekben ezek a részecskék elhelyezkedhetnek, megközelítőleg megegyezik egy googolplexszel.
- Most képzelje el, hogy a googolplex nem is homokszem, hanem egy aprócska pont, amely csak a legerősebb mikroszkópon keresztül látható. És az egész univerzumunk tele van ilyen apró pontokkal. Tehát még ez sem hasonlítható össze Graham számával. De mi van, ha a megfigyelhető univerzum teljes terét fel akarjuk használni annak rögzítésére (tegyük fel, hogy az egyes számjegyek rögzítése legalább Planck kötetét foglalja el)? Jaj, ez nekünk nem fog menni! De mindig lehet más irányba menni.
Hogyan írhatunk G64-et Knuth módszerével
1976-ban Donald Knuth amerikai tudós javasolta a szuperfokok fogalmát vagy Knuth jelölését. Ez egy olyan módszer, amely lehetővé teszi, hogy nagyon nagy számokat írjon a felfelé mutató nyilak segítségével. A hatványozást egy felfelé mutató nyíl jelzi: ↑.
Így néz ki ez a jelölés: a ↑ b = ab = a × a × a ×… és így tovább b-szer.
- Például 3 ↑ 3 = 3 3.
- A Google-t így írják: 10 ↑ 10 ↑ 2.
- És googolplex - 10., 10., 10., 2.
A felfelé mutató nyilak fontos jellemzője, hogy nagyon gyorsan növekednek. Az expozíció sokkal gyorsabban növekszik, mint a szorzás. A 2 × 10 csak 20, de 2 ↑ 10 = 1024. Ugyanígy a nyilak minden új szintje sokkal gyorsabban növekszik, mint az előző szint.
Ha mentálisan elképzeled a 3 ↑↑↑ 4 hármasokból álló erőtornyot, akkor a Földtől a Marsig terjedő méretű szerkezetet kapsz. De még el sem értük azt az „alsó fokot”, amely Graham számához vezet.
Leírhatjuk Graham számát ezen felfelé mutató nyilak hatalmas készletével.
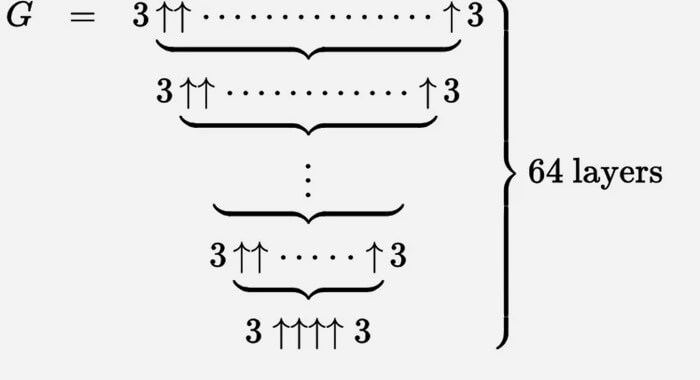
A legkönnyebb ezt iteratív folyamatként elképzelni. Alulról kezdjük, ahol g 1 = 3, 3, majd hozzunk létre egy második sort (nevezzük g 2-nek), ahol g 1 nyilak vannak a hármasok között.
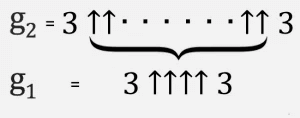
Ekkor g 3 két hármas, amelyeket g 2 felfelé mutató nyilak választanak el, és így tovább, amíg a g 64 és a hármasok közötti g 63 nyilakkal Graham-szám lesz.
Ha a halhatatlanság helyett a Graham-számmal megegyező élettartamot választ, akkor az eredmény majdnem ugyanaz lesz. Még ha feltételezzük is, hogy az Univerzumban, a Naprendszerben és a Földön a körülmények örökre változatlanok maradnak, az emberi agy nem tudna ilyen hosszú ideig ellenállni káros változások nélkül.

