Vjeruje se da je koncept brojeva prvi put nastao kad su prapovijesni ljudi počeli prstima nešto računati. Od tada je čovječanstvo daleko napredovalo. Sada koristimo kalkulatore i računala za brojanje najvećih brojeva. Pa čak su se pojavila i imena za brojeve koji su toliko veliki da ih je teško zamisliti.
Beskonačnost brojivih brojeva
Čini se da je odgovor na pitanje koji je najveći broj u matematici vrlo jednostavan. Beskonačnost, zar ne? Ali to nije posve točno. Napokon, beskonačnost uopće nije broj, već pojam. Ideja.
Beskonačnost (infinitum) je pojam koji u prijevodu s latinskog znači "bez granica". Definicija beskonačnosti u matematici kaže da bez obzira koliko je velik broj, uvijek mu možete dodati 1 i on će postati veći.
Stoga, strogo govoreći, ne postoji najveći broj na svijetu. Možete imenovati samo najveći broj s određenim imenom.
Neka od poznatijih imena za veliki broj su:
| Broj nula | Ime | Ime na engleskom |
|---|---|---|
| 3 | tisuću | tisuću |
| 6 | milijuna | milijuna |
| 9 | milijarda (milijarda) | milijarde |
| 12 | bilijuna | bilijuna |
| 15 | kvadrilion | kvadrilion |
| 18 | kvintilion | kvintilion |
| 21 | sekstilion | sekstilion |
| 24 | septillion | septillion |
| 27 | oktilion | oktilion |
| 30 | kvintilion | nonillion |
| 33 | deciliona | deciliona |
| 36 | nedecilion | nedecilion |
| 39 | duodekilion | duodekilion |
| 42 | tredecilion | tredecilion |
| 45 | četverokuta | quattuordecillion |
| 48 | petindecilion | petindeciliona |
| 51 | sexdecillion | sexdecillion |
| 54 | septendecillion | septendecillion |
| 57 | octodecillion | octodecillion |
| 60 | novemdecillion | novemdecillion |
| 63 | vigintilion | vigintilion |
| 66 | nevigintilion | nevigintilion |
| 69 | duovigintilion | duovigintilion |
| 72 | trevigintilion | trevigintilion |
| 75 | quatuorvigintillion | quattuorvigintillion |
| 78 | kvinvigintilion | kvinvigintilion |
| 81 | sexvigintillion | sexvigintillion |
| 84 | septenvigintillion | septenvigintillion |
| 87 | oktovigintilion | oktovigintilion |
| 90 | novemvigintillion | novemvigintillion |
| 93 | trigintilion | trigintilion |
| 96 | netrigintilion | netrigintilion |
| 99 | duotrigintilion | duotrigintilion |
| 102 | tretrigintilion | trestrigintilion |
| 105 | quattrigintillion | quattuortrigintillion |
| 108 | kvintrigintilion | kvintrigintilion |
| 111 | sextrigintillion | sextrigintillion |
| 114 | septentrigintillion | septentrigintillion |
| 117 | oktotrigintilion | oktotrigintilion |
| 120 | novemtrigintillion | novemtrigintillion |
| 123 | kvadragintilion | kvadragintilion |
| 126 | nekvadragintilion | nekvadragintilion |
| 129 | duoquadragintillion | duoquadragintillion |
| 132 | trackquadragintillion | trekvadragintilion |
| 135 | kvatorkvadragintilion | quattuorquadragintillion |
| 138 | kvinkvadragintilion | kvinkvadragintilion |
| 141 | sexquadragintillion | sexquadragintillion |
| 144 | septinkvadraginilion | septenquadragintillion |
| 147 | oktokvadragintilion | oktokvadragintilion |
| 150 | novemquadragintillion | novemquadragintillion |
| 153 | kvinkvagintilion | kvinkvagintilion |
| 156 | unquincagintillion | nekvinquagintilion |
| 159 | duoquincagintillion | duoquinquagintillion |
| 162 | trequincagintillion | trequinquagintillion |
| 165 | quatorquincagintillion | quattuorquinquagintillion |
| 168 | quinquincagintillion | quinquinquagintillion |
| 171 | sexquincagintillion | sexquinquagintillion |
| 174 | septenquincagintillion | septenquinquagintillion |
| 177 | oktoquincagintillion | oktokvinkvagintilion |
| 180 | novemquincagintillion | novemquinquagintillion |
| 183 | seksagintilion | seksagintilion |
| 186 | neseksagintilion | neseksagintilion |
| 189 | duoseksagintilion | duoseksagintilion |
| 192 | treseksagintilion | treseksagintilion |
| 195 | quatorsexagintillion | quattuorsexagintillion |
| 198 | kinseksagintilion | kinseksagintilion |
| 201 | sexsexagintillion | sexsexagintillion |
| 204 | septenseksagintilion | septenseksagintilion |
| 207 | oktoksaksagintilion | oktoksaksagintilion |
| 210 | novemsexagintillion | novemsexagintillion |
| 213 | septagintilion | septuagintilion |
| 216 | neseptagintilion | neseptuagintilion |
| 219 | duoseptagintilion | duoseptuagintillion |
| 222 | treseptagintilion | treseptuagintillion |
| 225 | kvatorseptagintilion | quattuorseptuagintillion |
| 228 | kvinseptagintilion | kvinseptuagintilion |
| 231 | sexseptagintillion | sexseptuagintillion |
| 234 | septenseptagintilion | septenseptuagintillion |
| 237 | oktozeptagintilion | oktoseptuagintilion |
| 240 | novemseptagintillion | novemseptuagintillion |
| 243 | oktogintilion | oktogintilion |
| 246 | unoctogintillion | unoctogintillion |
| 249 | duooctogintillion | duooctogintillion |
| 252 | tracktogintillion | treoktogintilion |
| 255 | kvatoroktogintilion | quattuoroctogintillion |
| 258 | kvinoktogintilion | kvinoktogintilion |
| 261 | seksoktogintilion | seksoktogintilion |
| 264 | septoktogintillion | septoctogintillion |
| 267 | oktoktogintilion | oktooktogintilion |
| 270 | novemoctogintillion | novemoctogintillion |
| 273 | nonagintilion | nonagintilion |
| 276 | nenagintilitet | nenagintilitet |
| 279 | duononagintilion | duononagintilion |
| 282 | trenonagintilion | trenonagintilion |
| 285 | quatornonagintillion | quattuornonagintillion |
| 288 | kvinonagintilion | kinonagintilion |
| 291 | seksnagintilion | seksnonagintilion |
| 294 | septennonagintilion | septennonagintilion |
| 297 | oktononagintilion | oktononagintilion |
| 300 | novemnonagintillion | novemnonagintillion |
| 303 | centilija | centilija |
Kako se zove najveći prosti broj
 Prosti broj je onaj koji je djeljiv samo sam po sebi i jedan. Krajem 2018. Amerikanac Patrick Laroche predstavio je najveći prosti broj znanstvenom svijetu.
Prosti broj je onaj koji je djeljiv samo sam po sebi i jedan. Krajem 2018. Amerikanac Patrick Laroche predstavio je najveći prosti broj znanstvenom svijetu.
- Njegova duljina iznosi 24.862.048 znakova. Za usporedbu: u epohalnom djelu L.N. Tolstojev "Rat i mir" ima oko 6-7 milijuna znakova ako uključite interpunkciju i razmake.
- Ovaj se broj može zapisati na sljedeći način: 282589933-1
- A glasi ovako: dva u snagu 82589933 minus jedan.
- Postoji čitav mrežni projekt GIMPS, usmjeren točno na pronalaženje najvećih prostih brojeva. U njemu sudjeluju matematičari iz različitih zemalja. Stoga se novi nositelji zapisa pojavljuju često. Znanstvenici rade, kako kažu, ne iz straha, već zbog novca. Napokon, tko god otvori sljedeći najveći Mersenne prime, dobit će 3000 dolara.
Koji je najveći broj na svijetu
 1980. godine Guinnessova knjiga rekorda uključila je Grahamov broj (poznat i kao G64 ili G), nazvan po američkom matematičaru Ronaldu Grahamu. To je najveći broj koji se ikad koristio u važnom matematičkom dokazu. Govorimo o teoriji Franka Ramseyja.
1980. godine Guinnessova knjiga rekorda uključila je Grahamov broj (poznat i kao G64 ili G), nazvan po američkom matematičaru Ronaldu Grahamu. To je najveći broj koji se ikad koristio u važnom matematičkom dokazu. Govorimo o teoriji Franka Ramseyja.
Ukratko o ovoj teoriji: zamislite N-dimenzionalnu kocku čiji su vrhovi nasumično povezani crvenim ili plavim segmentima crta. A naša je zadaća razumjeti do koje je vrijednosti N moguće (ako bojimo rubove kocke na različite načine), kako bismo izbjegli situaciju u kojoj će jedna ravnina u kocki biti obojana istom bojom. Odnosno, ne bismo trebali dobiti jednobojnu "omotnicu".
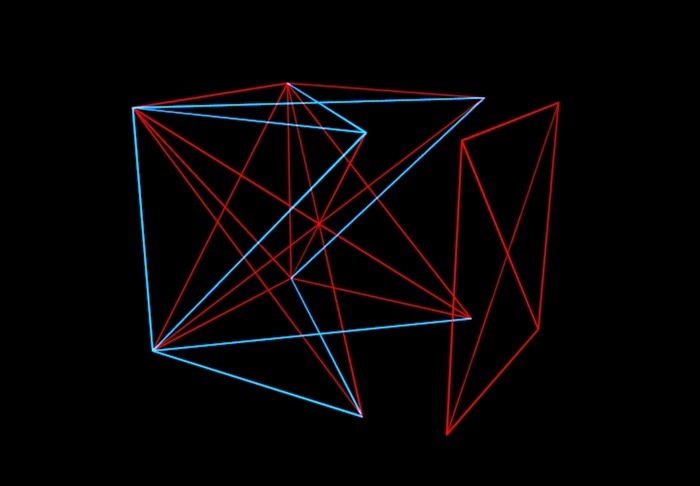
Matematičari su oslikali kocku na taj način i pokazalo se da do šestodimenzionalne kocke možete izmisliti i učiniti da linije iste boje koje povezuju četiri vrha ne leže u istoj ravnini. No sa sedmerodimenzionalnim, kako su doznali Graham i Rothschild, takav trik više nije moguć. I s osmodimenzionalnim. I ... "i tako dalje", što, međutim, nije beskonačno, već završava fantastično gigantskim brojem. To zovu Grahamov broj. Inače, rješenje Grahama i Rothschilda sada je zastarjelo. Matematičari su otkrili da se 6-7-8-9-10-11-11-12-dimenzionalne kocke i dalje mogu slikati bez omotnica. Ali negdje između 13 i Grahamovog broja, zacijelo postoji broj iznad kojeg će u svakom slučaju biti "omotnice".
Grahamov broj stekao je svjetsko priznanje 1977. godine kada je poznati popularizator znanosti Martin Gardner o tome napisao u časopisu Scientific American.
I premda su od tada bili i drugi kandidati za titulu najvećeg broja iz matematike, Grahamovo "umotvorina" najpopularnije je i najpoznatije. A ako ste čuli za "obitelj ugljena":
- googol - 10100;
Ili: 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 - googolplex - 10googol,
tada biste trebali znati da se ti brojevi u matematici samo "gnječe", a Grahamov broj je nezamisliv broj puta veći od njih. Pa čak i više od broja Skuse između 1019 i 1.3971672 10316 i približno jednaka e727,951336108.
Zanimljivo je da je izumom googola američki matematičar Edward Kazner studentima želio pokazati razliku između nevjerojatno velikog broja i beskonačnosti. Tada bi Grahamov broj mogao samo "razbiti glavu".
Je li moguće zamisliti i zapisati broj koji se ne može razumjeti
Matematičari vam neće moći reći točan broj znamenki u Grahamovom broju, a kamoli da mu se računaju. Poznato je samo posljednjih 50 znamenki najvećeg broja na svijetu - ovo je ... 03222348723967018485186439059104575627262464195387.
No, brojevi s kojima G64 počinje nepoznati su, a vjerojatno i neće biti.
Usporedimo tri čudovišta: googol, googolplex i Grahamov broj.
- Googol je broj zrna pijeska koji mogu stati u svemir, pomnožen s 10 milijardi.Dakle, zamislite svemir ispunjen sitnim zrncima pijeska - desetke milijardi svjetlosnih godina iznad Zemlje, ispod nje, ispred nje, iza nje - beskrajni pijesak.
Sad zamislite da u nekom trenutku uzmete jedno zrno pijeska da biste ga ispitali pod moćnim mikroskopom. I vidite da zapravo to nije jedino zrno, već 10 milijardi mikroskopskih zrna, a sve zajedno su veličine zrna pijeska. Da je to slučaj za svako pojedinačno zrnce pijeska u ovom hipotetičkom svemiru, tada bi ukupan iznos tih mikroskopskih zrna bio googol.
- Kako bi kvantificirao googolplex, astronom i astrofizičar Carl Sagan dao je primjer punjenja cijelog volumena promatranog svemira finim česticama prašine veličine približno 1,5 mikrometara. Na temelju toga, ukupan broj različitih kombinacija u kojima se ove čestice mogu nalaziti bit će približno jednak jednom googolplexu.
- Sad zamislite da googolplex nije niti zrno pijeska, već sićušna točka koja se može vidjeti samo najmoćnijim mikroskopom. I cijeli je naš svemir ispunjen tako sitnim točkicama. Dakle, čak ni ovo nije usporedivo s Grahamovim brojem. Ali što ako želimo koristiti cijeli prostor promatranog svemira da ga zabilježimo (pretpostavimo da bilježenje svake znamenke zauzima barem Planckov volumen)? Jao, ovo nam neće uspjeti! Ali uvijek možete ići drugim putem.
Kako napisati G64 Knuthovom metodom
1976. američki znanstvenik Donald Knuth predložio je koncept super stupnjeva ili Knuthovu notaciju. Ovo je metoda koja vam omogućuje pisanje vrlo velikih brojeva pomoću strelica usmjerenih prema gore. Pojačavanje je prikazano jednom strelicom prema gore: ↑.
Ovako izgleda ovaj zapis: a ↑ b = ab = a × a × a ×…, i tako dalje b puta.
- Na primjer 3 ↑ 3 = 3³.
- Googol je zapisan kao 10 ↑ 10 ↑ 2.
- Googolplex - 10 ↑ 10 ↑ 10 ↑ 2
Važna značajka strelica prema gore je da rastu vrlo brzo. Izloženost raste mnogo brže od množenja. 2 × 10 je samo 20, ali 2 ↑ 10 = 1024. Na isti način, svaka nova razina strelica raste puno brže od prethodne razine.
Ako mentalno zamislite moćni toranj trojki 3 ↑↑↑ 4, dobit ćete strukturu veličine od Zemlje do Marsa. Ali nismo stigli ni do “donje prečke” koja nas vodi do Grahamovog broja.
Grahamov broj možemo opisati ogromnim skupom ovih strelica prema gore.
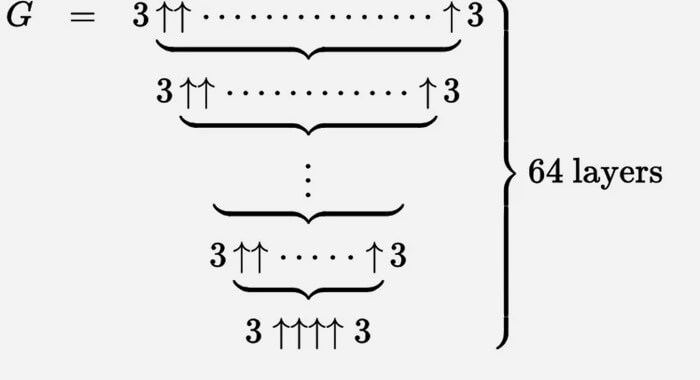
Najlakše je o tome razmišljati kao o iterativnom procesu. Počinjemo na dnu s g 1 = 3 ↑↑↑↑ 3, a zatim stvorimo drugi red (nazovimo ga g 2) sa g 1 strelicama između trojki.
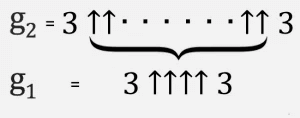
Tada su g 3 dvije trojke, odvojene g 2 strelicama prema gore, i tako dalje, sve dok g 64 sa strelice g 63 između trojki ne postane Grahamov broj.
Ako odaberete životni vijek jednak Grahamovom broju umjesto besmrtnosti, rezultat će biti gotovo isti. Čak i ako pretpostavimo da će uvjeti u Svemiru, u Sunčevom sustavu i na Zemlji zauvijek ostati nepromijenjeni, ljudski mozak ne bi mogao podnijeti tako dugo razdoblje bez štetnih promjena.

