It is believed that the concept of numbers first originated when prehistoric people began to use their fingers to count something. Since then, humanity has come a long way. We now use calculators and computers to count the largest numbers. And even names have appeared for numbers that are so large that they can hardly be imagined.
Infinity of countable numbers
It would seem that the answer to the question of what is the largest number in mathematics is very simple. Infinity, right? But this is not entirely correct. After all, infinity is not a number at all, but a concept. Idea.
Infinity (infinitum) is a concept that in translation from Latin means "without borders". The definition of infinity in mathematics says that no matter how large a number is, you can always add 1 to it and it will get bigger.
Therefore, strictly speaking, there is no such thing as the largest number in the world. You can only name the largest number given a specific name.
Some of the more well-known names for large numbers are:
| Number of zeros | Name | Name in English |
|---|---|---|
| 3 | thousand | thousand |
| 6 | million | million |
| 9 | billion (billion) | billion |
| 12 | trillion | trillion |
| 15 | quadrillion | quadrillion |
| 18 | quintillion | quintillion |
| 21 | sextillion | sextillion |
| 24 | septillion | septillion |
| 27 | octillion | octillion |
| 30 | quintillion | nonillion |
| 33 | decillion | decillion |
| 36 | undecillion | undecillion |
| 39 | duodecillion | duodecillion |
| 42 | tredecillion | tredecillion |
| 45 | quatuorddecillion | quattuordecillion |
| 48 | quindecillion | quindecillion |
| 51 | sexdecillion | sexdecillion |
| 54 | septendecillion | septendecillion |
| 57 | octodecillion | octodecillion |
| 60 | novemdecillion | novemdecillion |
| 63 | vigintillion | vigintillion |
| 66 | unvigintillion | unvigintillion |
| 69 | duovigintillion | duovigintillion |
| 72 | trevigintillion | trevigintillion |
| 75 | quatuorvigintillion | quattuorvigintillion |
| 78 | quinvigintillion | quinvigintillion |
| 81 | sexvigintillion | sexvigintillion |
| 84 | septenvigintillion | septenvigintillion |
| 87 | octovigintillion | octovigintillion |
| 90 | novemvigintillion | novemvigintillion |
| 93 | trigintillion | trigintillion |
| 96 | untrigintillion | untrigintillion |
| 99 | duotrigintillion | duotrigintillion |
| 102 | tretrigintillion | trestrigintillion |
| 105 | quattrigintillion | quattuortrigintillion |
| 108 | quintrigintillion | quintrigintillion |
| 111 | sextrigintillion | sextrigintillion |
| 114 | septentrigintillion | septentrigintillion |
| 117 | octotrigintillion | octotrigintillion |
| 120 | novemtrigintillion | novemtrigintillion |
| 123 | quadragintillion | quadragintillion |
| 126 | unquadragintillion | unquadragintillion |
| 129 | duoquadragintillion | duoquadragintillion |
| 132 | trackquadragintillion | trequadragintillion |
| 135 | quatorquadragintillion | quattuorquadragintillion |
| 138 | quinquadragintillion | quinquadragintillion |
| 141 | sexquadragintillion | sexquadragintillion |
| 144 | septinquadragintillion | septenquadragintillion |
| 147 | octoquadragintillion | octoquadragintillion |
| 150 | novemquadragintillion | novemquadragintillion |
| 153 | quinquagintillion | quinquagintillion |
| 156 | unquincagintillion | unquinquagintillion |
| 159 | duoquincagintillion | duoquinquagintillion |
| 162 | trequincagintillion | trequinquagintillion |
| 165 | quatorquincagintillion | quattuorquinquagintillion |
| 168 | quinquincagintillion | quinquinquagintillion |
| 171 | sexquinkagintillion | sexquinquagintillion |
| 174 | septenquincagintillion | septenquinquagintillion |
| 177 | octoquincagintillion | octoquinquagintillion |
| 180 | novemquincagintillion | novemquinquagintillion |
| 183 | sexagintillion | sexagintillion |
| 186 | unsexagintillion | unsexagintillion |
| 189 | duosexagintillion | duosexagintillion |
| 192 | tresexagintillion | tresexagintillion |
| 195 | quatorsexagintillion | quattuorsexagintillion |
| 198 | quinsexagintillion | quinsexagintillion |
| 201 | sexsexagintillion | sexsexagintillion |
| 204 | septensexagintillion | septensexagintillion |
| 207 | octosexagintillion | octosexagintillion |
| 210 | novemsexagintillion | novemsexagintillion |
| 213 | septagintillion | septuagintillion |
| 216 | unseptagintillion | unseptuagintillion |
| 219 | duoseptagintillion | duoseptuagintillion |
| 222 | treseptagintillion | treseptuagintillion |
| 225 | quatorseptagintillion | quattuorseptuagintillion |
| 228 | quinseptagintillion | quinseptuagintillion |
| 231 | sexseptagintillion | sexseptuagintillion |
| 234 | septenseptagintillion | septenseptuagintillion |
| 237 | octoseptagintillion | octoseptuagintillion |
| 240 | novemseptagintillion | novemseptuagintillion |
| 243 | octogintillion | octogintillion |
| 246 | unoctogintillion | unoctogintillion |
| 249 | duooctogintillion | duooctogintillion |
| 252 | tracktogintillion | treoctogintillion |
| 255 | quatoroctogintillion | quattuoroctogintillion |
| 258 | quinoctogintillion | quinoctogintillion |
| 261 | sexoctogintillion | sexoctogintillion |
| 264 | septoktogintillion | septoctogintillion |
| 267 | octoctogintillion | octooctogintillion |
| 270 | novemoctogintillion | novemoctogintillion |
| 273 | nonagintillion | nonagintillion |
| 276 | unnonagintillion | unnonagintillion |
| 279 | duononagintillion | duononagintillion |
| 282 | trenonagintillion | trenonagintillion |
| 285 | quatornonagintillion | quattuornonagintillion |
| 288 | quinnonagintillion | quinnonagintillion |
| 291 | sexnagintillion | sexnonagintillion |
| 294 | septennonagintillion | septennonagintillion |
| 297 | octononagintillion | octononagintillion |
| 300 | novemnonagintillion | novemnonagintillion |
| 303 | centillion | centillion |
What is the name of the largest prime number
 A prime number is one that is divisible only by itself and by one. At the end of 2018, the American Patrick Laroche presented the largest prime number to the scientific world.
A prime number is one that is divisible only by itself and by one. At the end of 2018, the American Patrick Laroche presented the largest prime number to the scientific world.
- Its length is 24,862,048 characters. For comparison: in the epoch-making work of L.N. Tolstoy's "War and Peace" is about 6-7 million characters, if you include punctuation and spaces.
- This number can be written as follows: 282589933-1
- And it reads like this: two to the power of 82589933 minus one.
- There is a whole online project GIMPS, aimed exactly at finding the largest primes. Mathematicians from different countries take part in it. Therefore, new record holders appear frequently. Scientists work, as they say, not for fear, but for money. After all, whoever opens the next largest Mersenne prime will get $ 3,000.
What is the largest number in the world
 In 1980, the Guinness Book of Records included the Graham number (also known as G64 or G), named after the American mathematician Ronald Graham. It is the largest number ever used in an important mathematical proof. We are talking about the theory of Frank Ramsey.
In 1980, the Guinness Book of Records included the Graham number (also known as G64 or G), named after the American mathematician Ronald Graham. It is the largest number ever used in an important mathematical proof. We are talking about the theory of Frank Ramsey.
Briefly about this theory: imagine an N-dimensional cube, its vertices are randomly connected by red or blue line segments. And our task is to understand up to what value of N it is possible (if the edges of the cube are painted in different ways), to avoid a situation in which one plane in the cube will be painted with one color. That is, we should not get a one-color "envelope".
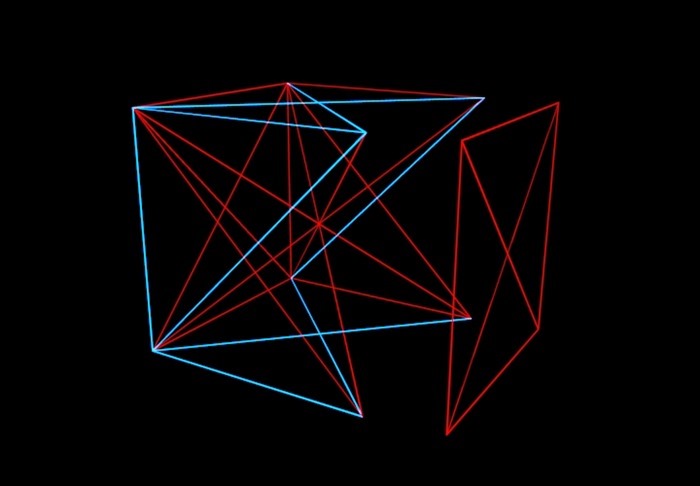
Mathematicians painted the cube this way and that, it turned out that up to a six-dimensional cube, you can contrive and make the lines of the same color connecting the four vertices not lie in the same plane. But with the seven-dimensional, as Graham and Rothschild found out, such a trick is no longer possible. And with an eight-dimensional. And ... "and so on", which, however, is not infinite, but ends with a fantastically gigantic number. This is what they call Graham's number. By the way, the solution by Graham and Rothschild is now outdated. Mathematicians have found out that 6-7-8-9-10-11-12-dimensional cubes can still be painted without envelopes. But somewhere between 13 and Graham's number, there is guaranteed to be a number above which "envelopes" will be in any case.
Graham's number gained worldwide recognition in 1977 when renowned popularizer of science Martin Gardner wrote about it in Scientific American.
And although since then there have been other candidates for the title of the largest number in mathematics, Graham's "brainchild" is the most popular and well-known. And if you've heard about the "coal family":
- googol - 10100;
Or: 10,000,000,000,000,000,000,000,000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 - googolplex - 10googol,
then you should know that these numbers in mathematics are just "kneading", and Graham's number is an unthinkable number of times greater than they. And even more than a Skuse number between 1019 and 1.3971672 10316 and approximately equal e727,951336108.
Curiously, by inventing googol, American mathematician Edward Kazner wanted to show students the difference between an incredibly large number and infinity. Then Graham's number might just "blow your mind."
Is it possible to imagine and write down a number beyond understanding
Mathematicians won't be able to tell you the exact number of digits in Graham's number, let alone count to him. Only the last 50 digits of the largest number in the world are known - this is ... 03222348723967018485186439059104575627262464195387.
But the numbers with which the G64 begins are unknown, and are unlikely to ever be.
Let's compare three monsters: googol, googolplex, and Graham's number.
- Googol is the number of grains of sand that can fit in the universe, multiplied by 10 billion.So, imagine a universe filled with small grains of sand - tens of billions of light years above the Earth, below it, in front of it, behind it - endless sand.
Now imagine that at some point you take one grain of sand to examine it under a powerful microscope. And you see that in fact this is not the only grain, but 10 billion microscopic grains, and together they are the size of a grain of sand. If that were the case for every single grain of sand in this hypothetical universe, then the total of these microscopic grains would be a googol.
- To quantify the googolplex, astronomer and astrophysicist Carl Sagan gave an example of filling the entire volume of the observable universe with fine dust particles approximately 1.5 micrometers in size. Based on this, the total number of different combinations in which these particles can be located will be approximately equal to one googolplex.
- Now imagine that a googolplex is not even a grain of sand, but a tiny point that can only be seen through the most powerful microscope. And our entire universe is filled with such tiny dots. So, even this is not in any comparison with Graham's number. But what if we want to use the entire space of the observable universe to record it (suppose that recording each digit takes up at least the Planck volume)? Alas, this will not work for us! But you can always go the other way.
How to write G64 using Knuth's method
In 1976, American scientist Donald Knuth proposed the concept of superdegrees or Knuth's notation. This is a method that allows you to write very large numbers using the upward pointing arrows. Exponentiation is indicated by one arrow pointing up: ↑.
This is what this notation looks like: a ↑ b = ab = a × a × a ×…, and so on b times.
- For example 3 ↑ 3 = 3³.
- Googol is written like this 10 ↑ 10 ↑ 2.
- A googolplex - 10 ↑ 10 ↑ 10 ↑ 2
An important feature of the up arrows is that they grow very quickly. Exposure grows much faster than multiplication. 2 × 10 is only 20, but 2 ↑ 10 = 1024. In the same way, each new level of arrows grows much faster than the previous level.
If you mentally imagine a power tower of triplets 3 ↑↑↑ 4, you will get a structure ranging in size from Earth to Mars. But we have not even reached the “bottom rung” that leads us to Graham's number.
We can describe Graham's number with a huge set of these upward arrows.
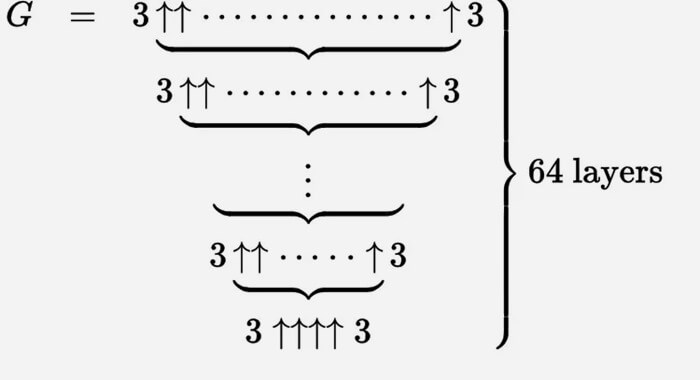
It is easiest to think of this as an iterative process. We start at the bottom with g 1 = 3 ↑↑↑↑ 3, and then create a second row (let's call it g 2) with g 1 arrows between the triplets.
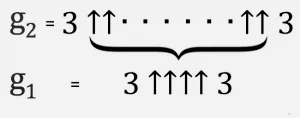
Then g 3 is two triples separated by g 2 with upward arrows and so on, until g 64 with g 63 arrows between the triples is a Graham number.
If you choose a lifespan equal to the Graham number instead of immortality, the result will be almost the same. Even if we assume that conditions in the Universe, in the Solar System and on Earth will forever remain unchanged, the human brain could not withstand such a long period of time without detrimental changes.

