Es wird angenommen, dass das Konzept der Zahlen zum ersten Mal entstand, als prähistorische Menschen begannen, mit den Fingern etwas zu zählen. Seitdem hat die Menschheit einen langen Weg zurückgelegt. Wir verwenden jetzt Taschenrechner und Computer, um die größten Zahlen zu zählen. Und sogar Namen sind für Zahlen aufgetaucht, die so groß sind, dass man sie sich kaum vorstellen kann.
Unendlichkeit zählbarer Zahlen
Es scheint, dass die Antwort auf die Frage nach der größten Zahl in der Mathematik sehr einfach ist. Unendlichkeit, richtig? Das ist aber nicht ganz richtig. Unendlichkeit ist schließlich überhaupt keine Zahl, sondern ein Konzept. Idee.
Unendlichkeit (infinitum) ist ein Konzept, das in der Übersetzung aus dem Lateinischen "ohne Grenzen" bedeutet. Die Definition von Unendlichkeit in der Mathematik besagt, dass Sie, egal wie groß eine Zahl ist, immer 1 hinzufügen können und sie größer wird.
Genau genommen gibt es daher nicht die größte Zahl der Welt. Sie können nur die größte Nummer mit einem bestimmten Namen benennen.
Einige der bekanntesten Namen für große Zahlen sind:
| Anzahl der Nullen | Name | Name in Englisch |
|---|---|---|
| 3 | tausend | tausend |
| 6 | Million | Million |
| 9 | Milliarden (Milliarden) | Milliarde |
| 12 | Billion | Billion |
| 15 | Billiarde | Billiarde |
| 18 | Trillion | Trillion |
| 21 | Sextillion | Sextillion |
| 24 | Septillion | Septillion |
| 27 | Oktillion | Oktillion |
| 30 | Trillion | Nonillion |
| 33 | Dezillion | Dezillion |
| 36 | Undecillion | Undecillion |
| 39 | Duodecillion | Duodecillion |
| 42 | tredecillion | tredecillion |
| 45 | quatuorddecillion | quattuordecillion |
| 48 | quindecillion | quindecillion |
| 51 | sexdecillion | sexdecillion |
| 54 | septendecillion | septendecillion |
| 57 | Oktodezillion | Oktodezillion |
| 60 | Novemdecillion | Novemdecillion |
| 63 | Vigintillion | Vigintillion |
| 66 | Unvigintillion | Unvigintillion |
| 69 | duovigintillion | duovigintillion |
| 72 | Trevigintillion | Trevigintillion |
| 75 | quatuorvigintillion | quattuorvigintillion |
| 78 | Quinvigintillion | Quinvigintillion |
| 81 | sexvigintillion | sexvigintillion |
| 84 | septenvigintillion | septenvigintillion |
| 87 | Octovigintillion | Octovigintillion |
| 90 | novemvigintillion | novemvigintillion |
| 93 | Trigintillion | Trigintillion |
| 96 | untrigintillion | untrigintillion |
| 99 | duotrigintillion | duotrigintillion |
| 102 | Tretrigintillion | trestrigintillion |
| 105 | quattrigintillion | quattuortrigintillion |
| 108 | Quintrigintillion | Quintrigintillion |
| 111 | sextrigintillion | sextrigintillion |
| 114 | Septentrigintillion | Septentrigintillion |
| 117 | Oktotrigintillion | Oktotrigintillion |
| 120 | novemtrigintillion | novemtrigintillion |
| 123 | Quadragintillion | Quadragintillion |
| 126 | unquadragintillion | unquadragintillion |
| 129 | duoquadragintillion | duoquadragintillion |
| 132 | trackquadragintillion | trequadragintillion |
| 135 | quatorquadragintillion | quattuorquadragintillion |
| 138 | Quinquadragintillion | Quinquadragintillion |
| 141 | sexquadragintillion | sexquadragintillion |
| 144 | Septinquadragintillion | septenquadragintillion |
| 147 | Octoquadragintillion | Octoquadragintillion |
| 150 | novemquadragintillion | novemquadragintillion |
| 153 | Quinquagintillion | Quinquagintillion |
| 156 | unquincagintillion | unquinquagintillion |
| 159 | duoquincagintillion | duoquinquagintillion |
| 162 | trequincagintillion | Trequinquagintillion |
| 165 | quatorquincagintillion | quattuorquinquagintillion |
| 168 | Quinquincagintillion | Chinquinquagintillion |
| 171 | sexquincagintillion | sexquinquagintillion |
| 174 | septenquincagintillion | septenquinquagintillion |
| 177 | Octoquincagintillion | Octoquinquagintillion |
| 180 | novemquincagintillion | novemquinquagintillion |
| 183 | sexagintillion | sexagintillion |
| 186 | unsexagintillion | unsexagintillion |
| 189 | duosexagintillion | duosexagintillion |
| 192 | tresexagintillion | tresexagintillion |
| 195 | quatorsexagintillion | quattuorsexagintillion |
| 198 | Quinsexagintillion | Quinsexagintillion |
| 201 | sexsexagintillion | sexsexagintillion |
| 204 | septensexagintillion | septensexagintillion |
| 207 | Octosexagintillion | Octosexagintillion |
| 210 | novemsexagintillion | novemsexagintillion |
| 213 | Septagintillion | Septuagintillion |
| 216 | unseptagintillion | unseptuagintillion |
| 219 | duoseptagintillion | duoseptuagintillion |
| 222 | treseptagintillion | treseptuagintillion |
| 225 | quatorseptagintillion | quattuorseptuagintillion |
| 228 | Quinseptagintillion | Quinseptuagintillion |
| 231 | sexseptagintillion | sexseptuagintillion |
| 234 | septenseptagintillion | septenseptuagintillion |
| 237 | Oktoseptagintillion | Octoseptuagintillion |
| 240 | novemseptagintillion | novemseptuagintillion |
| 243 | Oktogintillion | Oktogintillion |
| 246 | unoctogintillion | unoctogintillion |
| 249 | duooctogintillion | duooctogintillion |
| 252 | tracktogintillion | Treoctogintillion |
| 255 | quatoroktogintillion | quattuoroctogintillion |
| 258 | Quinoctogintillion | Quinoctogintillion |
| 261 | sexoctogintillion | sexoctogintillion |
| 264 | Septoktogintillion | Septoctogintillion |
| 267 | Octoctogintillion | Octooctogintillion |
| 270 | novemoctogintillion | novemoctogintillion |
| 273 | nonagintillion | nonagintillion |
| 276 | unnonagintillion | unnonagintillion |
| 279 | duononagintillion | duononagintillion |
| 282 | trenonagintillion | trenonagintillion |
| 285 | quatornonagintillion | quattuornonagintillion |
| 288 | Quinnonagintillion | Quinnonagintillion |
| 291 | sexnagintillion | sexnonagintillion |
| 294 | septennonagintillion | septennonagintillion |
| 297 | Octononagintillion | Octononagintillion |
| 300 | novemnonagintillion | novemnonagintillion |
| 303 | Centillion | Centillion |
Wie heißt die größte Primzahl?
 Eine Primzahl ist eine, die nur durch sich selbst und durch eins teilbar ist. Ende 2018 präsentierte der Amerikaner Patrick Laroche der wissenschaftlichen Welt die größte Primzahl.
Eine Primzahl ist eine, die nur durch sich selbst und durch eins teilbar ist. Ende 2018 präsentierte der Amerikaner Patrick Laroche der wissenschaftlichen Welt die größte Primzahl.
- Seine Länge beträgt 24.862.048 Zeichen. Zum Vergleich: In der epochalen Arbeit von L.N. Tolstois "Krieg und Frieden" besteht aus etwa 6-7 Millionen Zeichen, wenn Sie Interpunktion und Leerzeichen einschließen.
- Diese Nummer kann wie folgt geschrieben werden: 282589933-1
- Und es liest sich so: zwei hoch 82589933 minus eins.
- Es gibt ein ganzes Online-Projekt GIMPS, das genau darauf abzielt, die größten Primzahlen zu finden. Mathematiker aus verschiedenen Ländern nehmen daran teil. Daher erscheinen häufig neue Rekordhalter. Wissenschaftler arbeiten, wie sie sagen, nicht aus Angst, sondern für Geld. Denn wer die nächstgrößere Mersenne Prime eröffnet, bekommt 3.000 Dollar.
Was ist die größte Zahl der Welt
 1980 enthielt das Guinness-Buch der Rekorde die Graham-Nummer (auch als G64 oder G bekannt), benannt nach dem amerikanischen Mathematiker Ronald Graham. Es ist die größte Zahl, die jemals in einem wichtigen mathematischen Beweis verwendet wurde. Wir sprechen über die Theorie von Frank Ramsey.
1980 enthielt das Guinness-Buch der Rekorde die Graham-Nummer (auch als G64 oder G bekannt), benannt nach dem amerikanischen Mathematiker Ronald Graham. Es ist die größte Zahl, die jemals in einem wichtigen mathematischen Beweis verwendet wurde. Wir sprechen über die Theorie von Frank Ramsey.
Kurz zu dieser Theorie: Stellen Sie sich einen N-dimensionalen Würfel vor, dessen Eckpunkte zufällig durch rote oder blaue Liniensegmente verbunden sind. Und unsere Aufgabe ist es zu verstehen, bis zu welchem Wert von N es möglich ist (wenn die Kanten des Würfels auf unterschiedliche Weise gemalt werden), eine Situation zu vermeiden, in der eine Ebene im Würfel mit einer Farbe gemalt wird. Das heißt, wir sollten keinen einfarbigen "Umschlag" bekommen.
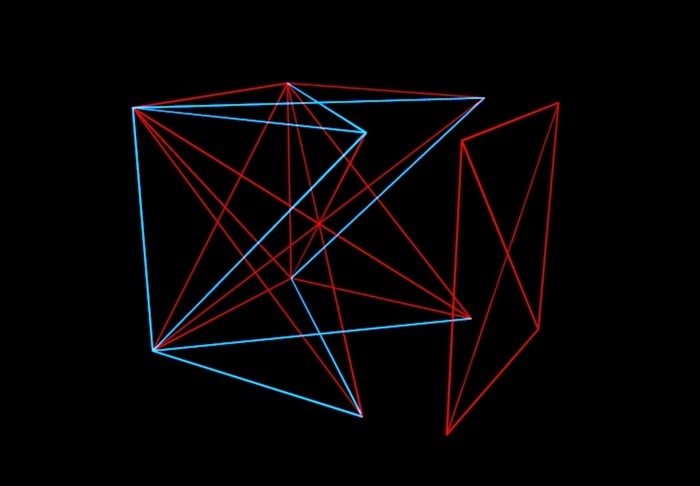
Mathematiker haben den Würfel so und so gemalt. Es stellte sich heraus, dass man bis zu einem sechsdimensionalen Würfel die Linien derselben Farbe erfinden und herstellen kann, die die vier Eckpunkte verbinden, die nicht in derselben Ebene liegen. Aber mit dem Siebendimensionalen ist, wie Graham und Rothschild herausfanden, ein solcher Trick nicht mehr möglich. Und mit einem achtdimensionalen. Und ... "und so weiter", was jedoch nicht unendlich ist, sondern mit einer fantastisch gigantischen Zahl endet. Das nennen sie Grahams Nummer. Übrigens ist die Lösung von Graham und Rothschild inzwischen veraltet. Mathematiker haben herausgefunden, dass 6-7-8-9-10-11-12-dimensionale Würfel immer noch ohne Umschläge gemalt werden können. Aber irgendwo zwischen 13 und Grahams Nummer gibt es garantiert eine Nummer, über der sich auf jeden Fall "Umschläge" befinden.
Grahams Nummer erlangte 1977 weltweite Anerkennung, als der renommierte Popularisator der Wissenschaft, Martin Gardner, in Scientific American darüber schrieb.
Und obwohl es seitdem andere Kandidaten für den Titel der größten Zahl in der Mathematik gegeben hat, ist Grahams "Idee" die beliebteste und bekannteste. Und wenn Sie von der "Kohlenfamilie" gehört haben:
- googol - 10100;
Oder: 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 - Googolplex - 10googol,
dann sollten Sie wissen, dass diese Zahlen in der Mathematik nur "kneten" und Grahams Zahl eine undenkbare Anzahl von Malen größer ist als sie. Und noch mehr als eine Skuse-Nummer zwischen 1019 und 1.3971672 10316 und ungefähr gleich e727,951336108.
Seltsamerweise wollte der amerikanische Mathematiker Edward Kazner mit der Erfindung von Googol den Schülern den Unterschied zwischen einer unglaublich großen Anzahl und einer Unendlichkeit zeigen. Dann könnte Grahams Nummer einfach "umhauen".
Ist es möglich, sich eine Zahl vorzustellen und aufzuschreiben, die unverständlich ist?
Mathematiker können Ihnen die genaue Anzahl der Ziffern in Grahams Nummer nicht sagen, geschweige denn für ihn zählen. Es sind nur die letzten 50 Ziffern der größten Zahl der Welt bekannt - dies ist ... 03222348723967018485186439059104575627262464195387.
Die Zahlen, mit denen der G64 beginnt, sind jedoch unbekannt und werden es wahrscheinlich nie sein.
Vergleichen wir drei Monster: Googol, Googolplex und Grahams Nummer.
- Googol ist die Anzahl der Sandkörner, die in das Universum passen, multipliziert mit 10 Milliarden.Stellen Sie sich also ein Universum vor, das mit kleinen Sandkörnern gefüllt ist - zig Milliarden Lichtjahre über der Erde, darunter, davor, dahinter - endloser Sand.
Stellen Sie sich nun vor, Sie nehmen irgendwann ein Sandkorn, um es unter einem leistungsstarken Mikroskop zu untersuchen. Und Sie sehen, dass dies tatsächlich kein einzelnes Korn ist, sondern 10 Milliarden mikroskopisch kleine Körner, und zusammen haben sie die Größe eines Sandkorns. Wenn dies für jedes einzelne Sandkorn in diesem hypothetischen Universum der Fall wäre, wäre die Summe dieser mikroskopisch kleinen Körner ein Googol.
- Zur Quantifizierung des Googolplex gab der Astronom und Astrophysiker Carl Sagan ein Beispiel für die Füllung des gesamten Volumens des beobachtbaren Universums mit Feinstaubpartikeln von etwa 1,5 Mikrometern Größe. Auf dieser Grundlage entspricht die Gesamtzahl der verschiedenen Kombinationen, in denen sich diese Partikel befinden können, ungefähr einem Googolplex.
- Stellen Sie sich nun vor, ein Googolplex ist nicht einmal ein Sandkorn, sondern ein winziger Punkt, der nur mit dem leistungsstärksten Mikroskop sichtbar ist. Und unser ganzes Universum ist mit so kleinen Punkten gefüllt. Selbst dies ist also nicht mit Grahams Zahl vergleichbar. Was aber, wenn wir den gesamten Raum des beobachtbaren Universums zur Aufzeichnung nutzen möchten (nehmen wir an, dass die Aufzeichnung jeder Ziffer mindestens das Planck-Volumen einnimmt)? Leider wird dies bei uns nicht funktionieren! Aber Sie können immer den anderen Weg gehen.
Wie man G64 mit Knuths Methode schreibt
1976 schlug der amerikanische Wissenschaftler Donald Knuth das Konzept der Supergrade oder Knuths Notation vor. Dies ist eine Methode, mit der Sie mit den nach oben zeigenden Pfeilen sehr große Zahlen schreiben können. Die Potenzierung wird durch einen Aufwärtspfeil angezeigt: ↑.
So sieht diese Notation aus: a ↑ b = ab = a × a × a ×… und so weiter b-mal.
- Zum Beispiel 3 ↑ 3 = 3³.
- Googol ist geschrieben als 10 ↑ 10 ↑ 2.
- Ein Googolplex - 10 ↑ 10 ↑ 10 ↑ 2
Ein wichtiges Merkmal der Aufwärtspfeile ist, dass sie sehr schnell wachsen. Die Belichtung wächst viel schneller als die Multiplikation. 2 × 10 ist nur 20, aber 2 ↑ 10 = 1024. Auf die gleiche Weise wächst jede neue Ebene von Pfeilen viel schneller als die vorherige Ebene.
Wenn Sie sich mental einen Kraftturm aus Drillingen 3 ↑↑↑ 4 vorstellen, erhalten Sie eine Struktur, deren Größe von der Erde bis zum Mars reicht. Aber wir haben noch nicht einmal die „unterste Sprosse“ erreicht, die uns zu Grahams Nummer führt.
Wir können Grahams Zahl mit einem riesigen Satz dieser Aufwärtspfeile beschreiben.
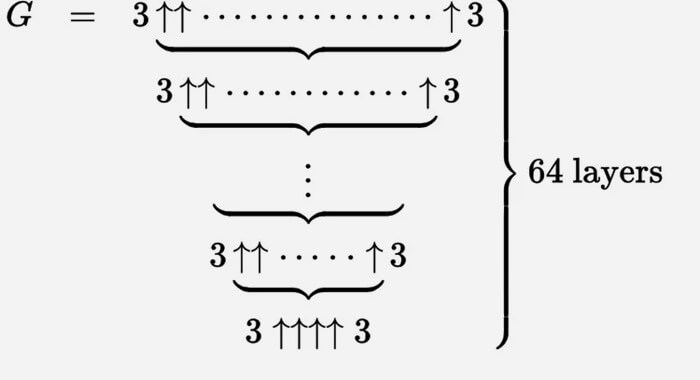
Es ist am einfachsten, sich dies als einen iterativen Prozess vorzustellen. Wir beginnen unten mit g 1 = 3 ↑↑↑↑ 3 und erstellen dann eine zweite Zeile (nennen wir sie g 2) mit g 1 -Pfeilen zwischen den Tripletts.
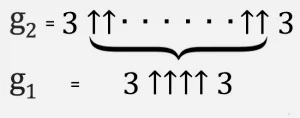
Dann ist g 3 zwei Tripel, die durch g 2 mit Aufwärtspfeilen usw. getrennt sind, bis g 64 mit g 63 Pfeilen zwischen den Tripeln eine Graham-Zahl ist.
Wenn Sie eine Lebensdauer wählen, die der Graham-Zahl anstelle der Unsterblichkeit entspricht, ist das Ergebnis fast dasselbe. Selbst wenn wir davon ausgehen, dass die Bedingungen im Universum, im Sonnensystem und auf der Erde für immer unverändert bleiben, könnte das menschliche Gehirn einer so langen Zeit ohne schädliche Veränderungen nicht standhalten.

