Det menes, at talbegrebet først opstod, da forhistoriske mennesker begyndte at bruge deres fingre til at tælle noget. Siden da er menneskeheden kommet langt. Vi bruger nu lommeregnere og computere til at tælle de største tal. Og endda navne har dukket op for numre, der er så store, at de næppe kan forestilles.
Uendelig antal tal
Det ser ud til, at svaret på spørgsmålet om, hvad der er det største antal i matematik, er meget simpelt. Uendelig, ikke? Men dette er ikke helt korrekt. Når alt kommer til alt er uendelighed slet ikke et tal, men et begreb. Ide.
Infinity (infinitum) er et begreb, der i oversættelse fra latin betyder "uden grænser". Definitionen af uendelighed i matematik siger, at uanset hvor stort et tal er, kan du altid tilføje 1 til det, og det bliver større.
Derfor er der strengt taget ikke noget som det største antal i verden. Du kan kun navngive det største nummer givet et specifikt navn.
Nogle af de mere berømte navne for store antal er:
| Antal nuller | Navn | Navn på engelsk |
|---|---|---|
| 3 | tusind | tusind |
| 6 | million | million |
| 9 | milliarder (milliarder) | milliard |
| 12 | billioner | billioner |
| 15 | kvadrillion | kvadrillion |
| 18 | kvintillion | kvintillion |
| 21 | sekstillion | sekstillion |
| 24 | septillion | septillion |
| 27 | octillion | octillion |
| 30 | kvintillion | nonillion |
| 33 | decillion | decillion |
| 36 | undecillion | undecillion |
| 39 | duodecillion | duodecillion |
| 42 | tredecillion | tredecillion |
| 45 | quatuorddecillion | quattuordecillion |
| 48 | quindecillion | quindecillion |
| 51 | sexdecillion | sexdecillion |
| 54 | septendecillion | septendecillion |
| 57 | octodecillion | octodecillion |
| 60 | novemdecillion | novemdecillion |
| 63 | vigintillion | vigintillion |
| 66 | unvigintillion | unvigintillion |
| 69 | duovigintillion | duovigintillion |
| 72 | trevigintillion | trevigintillion |
| 75 | quatuorvigintillion | quattuorvigintillion |
| 78 | quinvigintillion | quinvigintillion |
| 81 | sexvigintillion | sexvigintillion |
| 84 | septenvigintillion | septenvigintillion |
| 87 | octovigintillion | octovigintillion |
| 90 | novemvigintillion | novemvigintillion |
| 93 | trigintillion | trigintillion |
| 96 | untrigintillion | untrigintillion |
| 99 | duotrigintillion | duotrigintillion |
| 102 | tretrigintillion | trestrigintillion |
| 105 | quattrigintillion | quattuortrigintillion |
| 108 | kvintrigintillion | kvintrigintillion |
| 111 | sekstrigintillion | sekstrigintillion |
| 114 | septentrigintillion | septentrigintillion |
| 117 | octotrigintillion | octotrigintillion |
| 120 | novemtrigintillion | novemtrigintillion |
| 123 | kvadragintillion | kvadragintillion |
| 126 | unquadragintillion | unquadragintillion |
| 129 | duoquadragintillion | duoquadragintillion |
| 132 | trackquadragintillion | trekvadragintillion |
| 135 | quatorquadragintillion | quattuorquadragintillion |
| 138 | quinquadragintillion | quinquadragintillion |
| 141 | sexquadragintillion | sexquadragintillion |
| 144 | septinquadragintillion | septenquadragintillion |
| 147 | octoquadragintillion | octoquadragintillion |
| 150 | novemquadragintillion | novemquadragintillion |
| 153 | quinquagintillion | quinquagintillion |
| 156 | unquincagintillion | uquinquagintillion |
| 159 | duoquincagintillion | duoquinquagintillion |
| 162 | trequincagintillion | trequinquagintillion |
| 165 | quatorquincagintillion | quattuorquinquagintillion |
| 168 | quinquincagintillion | quinquinquagintillion |
| 171 | sexquincagintillion | sexquinquagintillion |
| 174 | septenquincagintillion | septenquinquagintillion |
| 177 | octoquincagintillion | octoquinquagintillion |
| 180 | novemquincagintillion | novemquinquagintillion |
| 183 | sexagintillion | sexagintillion |
| 186 | unsexagintillion | unsexagintillion |
| 189 | duosagintillion | duosagintillion |
| 192 | tresexagintillion | tresexagintillion |
| 195 | quatorsexagintillion | quattuorsexagintillion |
| 198 | quinsexagintillion | quinsexagintillion |
| 201 | sexsexagintillion | sexsexagintillion |
| 204 | septensexagintillion | septensexagintillion |
| 207 | octosexagintillion | octosexagintillion |
| 210 | novemsexagintillion | novemsexagintillion |
| 213 | septagintillion | septuagintillion |
| 216 | unseptagintillion | unseptuagintillion |
| 219 | duoseptagintillion | duoseptuagintillion |
| 222 | treseptagintillion | treseptuagintillion |
| 225 | quatorseptagintillion | quattuorseptuagintillion |
| 228 | quinseptagintillion | quinseptuagintillion |
| 231 | sexseptagintillion | sexseptuagintillion |
| 234 | septenseptagintillion | septenseptuagintillion |
| 237 | octoseptagintillion | octoseptuagintillion |
| 240 | novemseptagintillion | novemseptuagintillion |
| 243 | octogintillion | octogintillion |
| 246 | unoctogintillion | unoctogintillion |
| 249 | duooctogintillion | duooctogintillion |
| 252 | tracktogintillion | treoctogintillion |
| 255 | quatoroktogintillion | quattuoroctogintillion |
| 258 | quinoctogintillion | quinoctogintillion |
| 261 | sexoctogintillion | sexoctogintillion |
| 264 | septoktogintillion | septoctogintillion |
| 267 | octoctogintillion | octooctogintillion |
| 270 | novemoctogintillion | novemoctogintillion |
| 273 | nonagintillion | nonagintillion |
| 276 | unnonagintillion | unnonagintillion |
| 279 | duononagintillion | duononagintillion |
| 282 | trenonagintillion | trenonagintillion |
| 285 | quatornonagintillion | quattuornonagintillion |
| 288 | quinnonagintillion | quinnonagintillion |
| 291 | sexnagintillion | sexnonagintillion |
| 294 | septennonagintillion | septennonagintillion |
| 297 | octononagintillion | octononagintillion |
| 300 | novemnonagintillion | novemnonagintillion |
| 303 | centillion | centillion |
Hvad er navnet på det største primtal
 Et primtal er et, der kun kan deles af sig selv og af et. I slutningen af 2018 præsenterede amerikaneren Patrick Laroche det største primtal for den videnskabelige verden.
Et primtal er et, der kun kan deles af sig selv og af et. I slutningen af 2018 præsenterede amerikaneren Patrick Laroche det største primtal for den videnskabelige verden.
- Dens længde er 24.862.048 tegn. Til sammenligning: i det epokerende arbejde af L.N. Tolstojs "Krig og fred" handler om 6-7 millioner tegn, hvis du inkluderer tegnsætning og mellemrum.
- Dette nummer kan skrives som følger: 282589933-1
- Og det læser sådan: to til magten 82589933 minus en.
- Der er et helt online-projekt GIMPS, der har til formål nøjagtigt at finde de største primtal. Matematikere fra forskellige lande deltager i det. Derfor vises nye rekordholdere ofte. Forskere arbejder, som de siger, ikke for frygt, men for penge. Når alt kommer til alt, den, der åbner den næststørste Mersenne-premier, får $ 3.000.
Hvad er det største antal i verden
 I 1980 inkluderede Guinness Book of Records Graham-nummeret (aka G64 eller G), opkaldt efter den amerikanske matematiker Ronald Graham. Det er det største antal, der nogensinde er brugt i et vigtigt matematisk bevis. Vi taler om teorien om Frank Ramsey.
I 1980 inkluderede Guinness Book of Records Graham-nummeret (aka G64 eller G), opkaldt efter den amerikanske matematiker Ronald Graham. Det er det største antal, der nogensinde er brugt i et vigtigt matematisk bevis. Vi taler om teorien om Frank Ramsey.
Kort om denne teori: forestil dig en N-dimensionel terning, dens hjørner er tilfældigt forbundet med røde eller blå linjesegmenter. Og vores opgave er at forstå op til, hvilken værdi af N det er muligt (hvis kanterne på terningen er malet på forskellige måder), for at undgå en situation, hvor et plan i terningen males med en farve. Det vil sige, vi skal ikke få en enfarvet "konvolut".
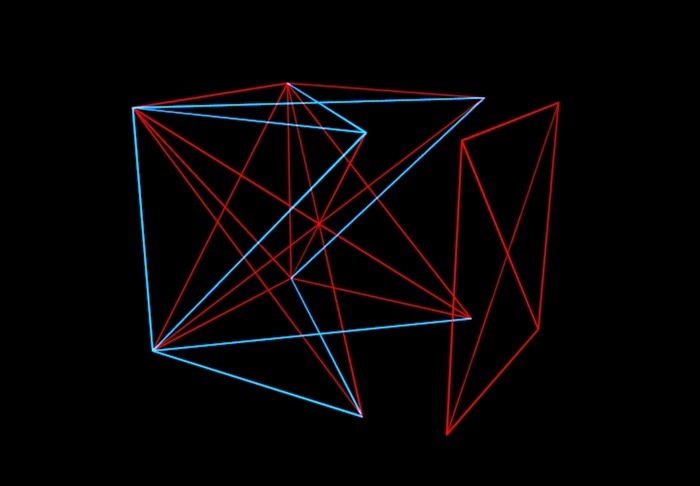
Matematikere malede terningen på denne måde og det, det viste sig, at op til en seksdimensional terning kan du undgå og få linjerne i samme farve, der forbinder de fire hjørner, ikke ligger i samme plan. Men med det syv-dimensionelle, som Graham og Rothschild fandt ud af, er et sådant trick ikke længere muligt. Og med en otte-dimensionel. Og ... "og så videre", som imidlertid ikke er uendelig, men ender med et fantastisk gigantisk antal. Dette er hvad de kalder Grahams nummer. Forresten er løsningen fra Graham og Rothschild nu forældet. Matematikere har fundet ud af, at 6-7-8-9-10-11-12-dimensionelle terninger stadig kan males uden konvolutter. Men et sted mellem 13 og Grahams nummer er der garanteret et nummer, hvorunder "konvolutter" under alle omstændigheder vil være.
Grahams nummer fik verdensomspændende anerkendelse i 1977, da den berømte popularisering af videnskaben Martin Gardner skrev om det i Scientific American.
Og selvom der siden da har været andre kandidater til titlen som det største antal i matematik, er Grahams "hjernebarn" den mest populære og velkendte. Og hvis du har hørt om "kulfamilien":
- googol - 10100;
Eller: 10.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 - googolplex - 10googol,
så skal du vide, at disse tal i matematik bare "ælter", og Grahams antal er et utænkeligt antal gange større end de. Og endda mere end et Skuse-nummer mellem 1019 og 1.3971672 10316 og omtrent ens e727,951336108.
Mærkeligt nok ville den amerikanske matematiker Edward Kazner ved at opfinde googol vise eleverne forskellen mellem et utroligt stort antal og uendeligt. Så kan Grahams nummer bare "sprænge dig i tankerne."
Er det muligt at forestille sig og skrive et tal ud over forståelse
Matematikere vil ikke være i stand til at fortælle dig det nøjagtige antal cifre i Grahams tal, endsige tælle for ham. Kun de sidste 50 cifre af det største antal i verden er kendt - dette er ... 03222348723967018485186439059104575627262464195387.
Men de numre, som G64 begynder med, er ukendte og vil sandsynligvis aldrig være.
Lad os sammenligne tre monstre: googol, googolplex og Grahams nummer.
- Googol er antallet af sandkorn, der kan passe i universet, ganget med 10 milliarder.Så forestil dig et univers fyldt med små sandkorn - snesevis af milliarder lysår over Jorden, under det, foran det, bag det - uendeligt sand.
Forestil dig nu, at du på et tidspunkt tager et sandkorn for at undersøge det under et kraftigt mikroskop. Og du ser, at dette faktisk ikke er det eneste korn, men 10 milliarder mikroskopiske korn, og alt sammen er de på størrelse med et sandkorn. Hvis det var tilfældet for hvert eneste sandkorn i dette hypotetiske univers, ville summen af disse mikroskopiske korn være en googol.
- For at kvantificere googolplexen gav astronom og astrofysiker Carl Sagan et eksempel på at fylde hele volumenet af det observerbare univers med fine støvpartikler på ca. 1,5 mikrometer i størrelse. Baseret på dette vil det samlede antal forskellige kombinationer, hvor disse partikler kan placeres, være omtrent lig med en googolplex.
- Forestil dig nu, at en googolplex ikke engang er et sandkorn, men et lille punkt, der kun kan ses gennem det mest kraftfulde mikroskop. Og hele vores univers er fyldt med så små prikker. Så selv dette er ikke i nogen sammenligning med Grahams nummer. Men hvad nu hvis vi vil bruge hele det observerbare univers til at optage det (antag at optagelse af hvert ciffer tager mindst Plancks volumen)? Ak, dette fungerer ikke for os! Men du kan altid gå den anden vej.
Sådan skriver du G64 ved hjælp af Knuths metode
I 1976 foreslog den amerikanske videnskabsmand Donald Knuth begrebet superdegrees eller Knuths notation. Dette er en metode, der giver dig mulighed for at skrive meget store tal ved hjælp af pilene, der peger opad. Eksponentiering er angivet med en pil, der peger opad: ↑.
Sådan ser denne betegnelse ud: a ↑ b = ab = a × a × a ×…, og så videre b gange.
- For eksempel 3 ↑ 3 = 3³.
- Googol er skrevet som 10 ↑ 10 ↑ 2.
- En googolplex - 10 ↑ 10 ↑ 10 ↑ 2
Et vigtigt træk ved pilene op er, at de vokser meget hurtigt. Eksponering vokser meget hurtigere end multiplikation. 2 × 10 er kun 20, men 2 ↑ 10 = 1024. På samme måde vokser hvert nye niveau af pile meget hurtigere end det foregående niveau.
Hvis du mentalt forestiller dig et krafttårn med tripletter 3 ↑↑↑ 4, får du en struktur, der varierer i størrelse fra Jorden til Mars. Men vi har ikke engang nået det "nederste trin", der fører os til Grahams nummer.
Vi kan beskrive Grahams nummer med et stort sæt af disse opadgående pile.
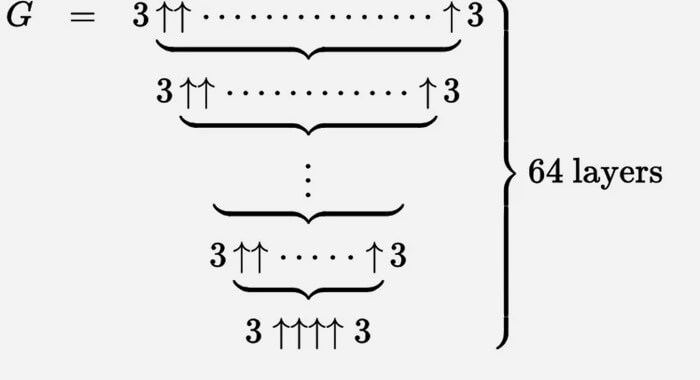
Det er nemmest at tænke på dette som en iterativ proces. Vi starter i bunden med g 1 = 3 ↑↑↑↑ 3, og opretter derefter en anden række (lad os kalde det g 2) med g 1 pile mellem tripletterne.
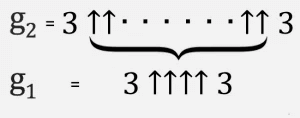
Derefter er g 3 to tredobler adskilt af g 2 med opadgående pile og så videre, indtil g 64 med g 63 pile mellem tredoblerne er et Graham-tal.
Hvis du vælger en levetid svarende til Graham-nummeret i stedet for udødelighed, bliver resultatet næsten det samme. Selv hvis vi antager, at forholdene i universet, i solsystemet og på jorden for evigt forbliver uændrede, kunne den menneskelige hjerne umuligt have udholdt en så lang periode uden skadelige ændringer.

