Předpokládá se, že koncept čísel poprvé vznikl, když pravěcí lidé začali pomocí prstů něco počítat. Od té doby prošlo lidstvo dlouhou cestou. K počítání největších čísel nyní používáme kalkulačky a počítače. A dokonce i jména se objevila u čísel, která jsou tak velká, že si je lze jen stěží představit.
Nekonečno spočetných čísel
Zdá se, že odpověď na otázku, jaké je největší číslo v matematice, je velmi jednoduchá. Nekonečno, že? Ale to není úplně správné. Nakonec, nekonečno není vůbec číslo, ale pojem. Nápad.
Nekonečno (infinitum) je pojem, který v překladu z latiny znamená „bez hranic“. Definice nekonečna v matematice říká, že bez ohledu na to, jak velké je číslo, vždy k němu můžete přidat 1 a zvětší se.
Striktně vzato tedy neexistuje nic jako největší počet na světě. Můžete pojmenovat pouze největší číslo s konkrétním jménem.
Některé ze slavnějších jmen pro velká čísla jsou:
| Počet nul | název | Název v angličtině |
|---|---|---|
| 3 | tisíc | tisíc |
| 6 | milión | milión |
| 9 | miliarda (miliarda) | miliarda |
| 12 | bilion | bilion |
| 15 | kvadrilion | kvadrilion |
| 18 | pětina | pětina |
| 21 | sextillion | sextillion |
| 24 | septillion | septillion |
| 27 | oktilion | oktilion |
| 30 | pětina | neillion |
| 33 | desetiletí | desetiletí |
| 36 | nerozhodnost | nerozhodnost |
| 39 | duodecillion | duodecillion |
| 42 | tredecillion | tredecillion |
| 45 | quatuorddecillion | quattuordecillion |
| 48 | quindecillion | quindecillion |
| 51 | sexdecillion | sexdecillion |
| 54 | septendecillion | septendecillion |
| 57 | octodecillion | octodecillion |
| 60 | novemdecillion | novemdecillion |
| 63 | vigintillion | vigintillion |
| 66 | nevigintilion | nevigintilion |
| 69 | duovigintillion | duovigintillion |
| 72 | trevigintillion | trevigintillion |
| 75 | quatuorvigintillion | quattuorvigintillion |
| 78 | quinvigintillion | quinvigintillion |
| 81 | sexvigintillion | sexvigintillion |
| 84 | septenvigintillion | septenvigintillion |
| 87 | octovigintillion | octovigintillion |
| 90 | novemvigintillion | novemvigintillion |
| 93 | trigintillion | trigintillion |
| 96 | Untrigintillion | Untrigintillion |
| 99 | duotrigintillion | duotrigintillion |
| 102 | tretrigintillion | trestrigintillion |
| 105 | quattrigintillion | quattuortrigintillion |
| 108 | quintrigintillion | quintrigintillion |
| 111 | sextrigintillion | sextrigintillion |
| 114 | septentrigintillion | septentrigintillion |
| 117 | octotrigintillion | octotrigintillion |
| 120 | novemtrigintillion | novemtrigintillion |
| 123 | quadragintillion | quadragintillion |
| 126 | unquadragintillion | unquadragintillion |
| 129 | duoquadragintillion | duoquadragintillion |
| 132 | trackquadragintillion | trequadragintillion |
| 135 | quatorquadragintillion | quattuorquadragintillion |
| 138 | quinquadragintillion | quinquadragintillion |
| 141 | sexquadragintillion | sexquadragintillion |
| 144 | septinquadragintillion | septenquadragintillion |
| 147 | octoquadragintillion | octoquadragintillion |
| 150 | novemquadragintillion | novemquadragintillion |
| 153 | quinquagintillion | quinquagintillion |
| 156 | unquincagintillion | unquinquagintillion |
| 159 | duoquincagintillion | duoquinquagintillion |
| 162 | trequincagintillion | trequinquagintillion |
| 165 | quatorquincagintillion | quattuorquinquagintillion |
| 168 | quinquincagintillion | quinquinquagintillion |
| 171 | sexquincagintillion | sexquinquagintillion |
| 174 | septenquincagintillion | septenquinquagintillion |
| 177 | octoquincagintillion | octoquinquagintillion |
| 180 | novemquincagintillion | novemquinquagintillion |
| 183 | sexagintillion | sexagintillion |
| 186 | unsexagintillion | unsexagintillion |
| 189 | duosexagintillion | duosexagintillion |
| 192 | tresexagintillion | tresexagintillion |
| 195 | quatorsexagintillion | quattuorsexagintillion |
| 198 | quinsexagintillion | quinsexagintillion |
| 201 | sexsexagintillion | sexsexagintillion |
| 204 | septensexagintillion | septensexagintillion |
| 207 | octosexagintillion | octosexagintillion |
| 210 | novemsexagintillion | novemsexagintillion |
| 213 | septagintillion | septuagintillion |
| 216 | unseptagintillion | nevyzpytatelný milion |
| 219 | duoseptagintillion | duoseptuagintillion |
| 222 | treseptagintillion | treseptuagintillion |
| 225 | quatorseptagintillion | quattuorseptuagintillion |
| 228 | quinseptagintillion | quinseptuagintillion |
| 231 | sexseptagintillion | sexseptuagintillion |
| 234 | septenseptagintillion | septenseptuagintillion |
| 237 | octoseptagintillion | octoseptuagintillion |
| 240 | novemseptagintillion | novemseptuagintillion |
| 243 | octogintillion | octogintillion |
| 246 | unoctogintillion | unoctogintillion |
| 249 | duooctogintillion | duooctogintillion |
| 252 | tracktogintillion | treoctogintillion |
| 255 | quatoroktogintillion | quattuoroctogintillion |
| 258 | chinoctogintillion | chinoctogintillion |
| 261 | sexoktologintilion | sexoktologintilion |
| 264 | septoktogintillion | septoctogintillion |
| 267 | octoctogintillion | octooctogintillion |
| 270 | novemoktologintilion | novemoktologintilion |
| 273 | nonagintillion | nonagintillion |
| 276 | nezasvěcený | nezasvěcený |
| 279 | duononagintillion | duononagintillion |
| 282 | trenonagintillion | trenonagintillion |
| 285 | quatornonagintillion | quattuornonagintillion |
| 288 | quinnonagintillion | quinnonagintillion |
| 291 | sexnagintillion | sexnonagintillion |
| 294 | septennonagintillion | septennonagintillion |
| 297 | octononagintillion | octononagintillion |
| 300 | novemnonagintillion | novemnonagintillion |
| 303 | centillion | centillion |
Jak se jmenuje největší prvočíslo
 Prvočíslo je číslo, které je dělitelné pouze samo sebou a jednou. Na konci roku 2018 představil Američan Patrick Laroche největší vědecké číslo.
Prvočíslo je číslo, které je dělitelné pouze samo sebou a jednou. Na konci roku 2018 představil Američan Patrick Laroche největší vědecké číslo.
- Jeho délka je 24 862 048 znaků. Pro srovnání: v epochální tvorbě L.N. Tolstého „Válka a mír“ má asi 6–7 milionů znaků, pokud zahrnete interpunkci a mezery.
- Toto číslo lze zapsat následovně: 282589933-1
- A zní to takto: dva na výkon 82589933 mínus jeden.
- Existuje celý online projekt GIMPS, jehož cílem je přesně najít největší prvočísla. Podílejí se na něm matematici z různých zemí. Proto se často objevují noví držitelé záznamů. Vědci pracují, jak se říká, ne kvůli strachu, ale kvůli penězům. Konec konců, kdokoli otevře další největší Mersenne prime, dostane 3 000 $.
Jaké je největší číslo na světě
 V roce 1980 Guinnessova kniha rekordů obsahovala Grahamovo číslo (aka G64 nebo G), pojmenované po americkém matematikovi Ronaldovi Grahamovi. Je to největší počet, jaký kdy byl použit v důležitém matematickém důkazu. Mluvíme o teorii Franka Ramseyho.
V roce 1980 Guinnessova kniha rekordů obsahovala Grahamovo číslo (aka G64 nebo G), pojmenované po americkém matematikovi Ronaldovi Grahamovi. Je to největší počet, jaký kdy byl použit v důležitém matematickém důkazu. Mluvíme o teorii Franka Ramseyho.
Stručně k této teorii: představte si N-dimenzionální krychli, její vrcholy jsou náhodně spojeny červenými nebo modrými úsečkami. A naším úkolem je pochopit, do jaké hodnoty N je možné (pokud budeme malovat přes okraje krychle různými způsoby), vyhnout se situaci, kdy bude jedna rovina v krychli natřena jednou barvou. To znamená, že bychom neměli dostávat jednobarevnou „obálku“.
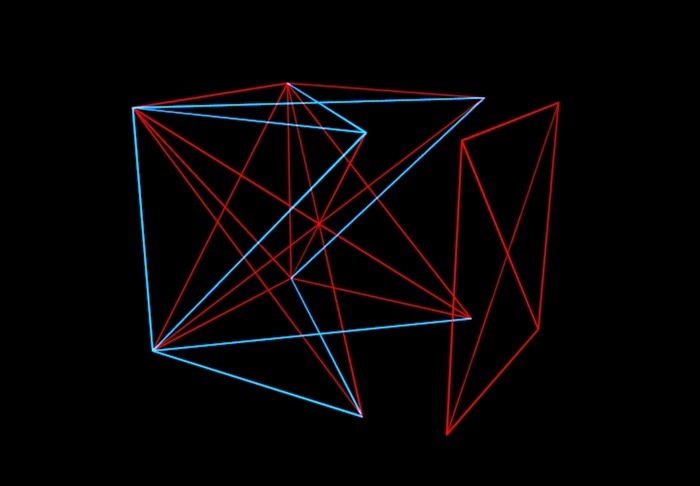
Matematici namalovali krychli tímto způsobem a ukázalo se, že až do šestimenzionální krychle můžete vymyslet a vytvořit čáry stejné barvy spojující čtyři vrcholy neleže ve stejné rovině. Ale s sedmrozměrným, jak zjistili Graham a Rothschild, takový trik již není možný. A s osmi-dimenzionální. A ... „a tak dále“, které však není nekonečné, ale končí fantasticky gigantickým číslem. Tomu říkají Grahamovo číslo. Mimochodem, řešení Grahama a Rothschilda je nyní zastaralé. Matematici zjistili, že 6-7-8-9-10-11-12-rozměrné kostky lze stále malovat bez „obálek“. Ale někde mezi 13 a Grahamovým číslem je zaručeno, že bude číslo, nad kterým budou „obálky“ v každém případě.
Grahamovo číslo získalo celosvětové uznání v roce 1977, kdy o tom napsal renomovaný popularizátor vědy Martin Gardner v časopise Scientific American.
A ačkoli od té doby existují i další kandidáti na titul největšího počtu v matematice, Grahamův „brainchild“ je nejoblíbenější a nejznámější. A pokud jste slyšeli o „uhelné rodině“:
- googol - 10100;
Nebo: 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 - googolplex - 10googol,
pak byste měli vědět, že tato čísla v matematice jsou pouze „hnětení“ a Grahamovo číslo je nepředstavitelně mnohokrát větší než oni. A dokonce více než číslo Skuse mezi 1019 a 1.3971672 10316 a přibližně stejné E727,951336108.
Je zajímavé, že vynálezem googolu chtěl americký matematik Edward Kazner ukázat studentům rozdíl mezi neuvěřitelně velkým počtem a nekonečnem. Potom by Grahamovo číslo mohlo „vyhodit z hlavy“.
Je možné si představit a zapsat číslo nad rámec pochopení
Matematici vám nebudou schopni říct přesný počet číslic v Grahamově čísle, natož aby se mu počítali. Je známo pouze posledních 50 číslic největšího počtu na světě - to je ... 03222348723967018485186439059104575627262464195387.
Čísla, s nimiž G64 začíná, jsou neznámá a sotva kdy budou.
Porovnejme tři příšery: googol, googolplex a Grahamovo číslo.
- Googol je počet zrn písku, které se vejdou do vesmíru, vynásobený 10 miliardami.Představte si tedy vesmír naplněný malými zrnky písku - desítky miliard světelných let nad Zemí, pod ní, před ní, za ní - nekonečný písek.
Nyní si představte, že v určitém okamžiku vezmete jedno zrnko písku, abyste jej prozkoumali pod silným mikroskopem. A vidíte, že ve skutečnosti nejde o jediné zrno, ale o 10 miliard mikroskopických zrn a dohromady mají velikost zrna písku. Pokud by tomu tak bylo pro každé jedno zrnko písku v tomto hypotetickém vesmíru, pak by součet těchto mikroskopických zrn byl googol.
- Pro kvantifikaci googolplexu dal astronom a astrofyzik Carl Sagan příklad naplnění celého objemu pozorovatelného vesmíru jemnými prachovými částicemi o velikosti přibližně 1,5 mikrometru. Na základě toho bude celkový počet různých kombinací, ve kterých mohou být tyto částice umístěny, přibližně stejný jako jeden googolplex.
- Nyní si představme, že googolplex není ani zrnko písku, ale malý bod, na který lze pohlížet pouze nejsilnějším mikroskopem. A celý náš vesmír je naplněn tak malými tečkami. Ani toto se tedy nesrovnává s Grahamovým číslem. Ale co když chceme k záznamu použít celý prostor pozorovatelného vesmíru (předpokládejme, že záznam každé číslice zabírá alespoň Planckův objem)? Bohužel to pro nás nebude fungovat! Vždy však můžete jít jinou cestou.
Jak psát G64 pomocí Knuthovy metody
V roce 1976 americký vědec Donald Knuth navrhl koncept superdegradů nebo Knuthovu notaci. Toto je metoda, která vám umožňuje psát velmi velká čísla pomocí šipek směřujících nahoru. Umocnění je označeno jednou šipkou směřující nahoru: ↑.
Takto vypadá tento zápis: a ↑ b = ab = a × a × a × ... atd. B krát.
- Například 3 ↑ 3 = 3³.
- Googol je zapsán jako 10 ↑ 10 ↑ 2.
- A googolplex - 10 ↑ 10 ↑ 10 ↑ 2
Důležitou vlastností šipek nahoru je, že rostou velmi rychle. Expozice roste mnohem rychleji než násobení. 2 × 10 je pouze 20, ale 2 ↑ 10 = 1024. Stejně tak každá nová úroveň šipek roste mnohem rychleji než předchozí úroveň.
Pokud si v duchu představíte energetickou věž trojčat 3 ↑↑↑ 4, získáte strukturu o velikosti od Země po Mars. Ale nedosáhli jsme ani „spodní příčky“, která nás vede k Grahamovu číslu.
Můžeme popsat Grahamovo číslo velkou sadou těchto šipek nahoru.
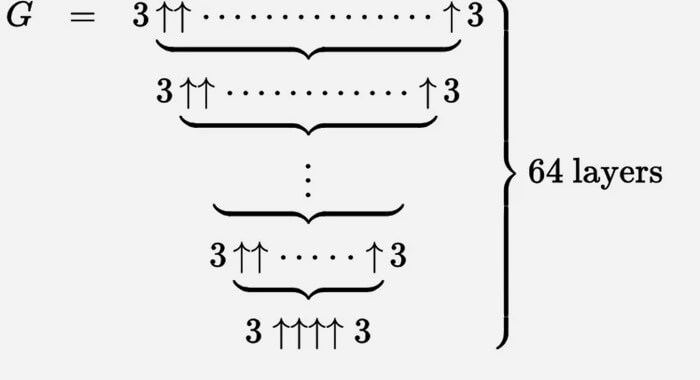
Je nejjednodušší si to představit jako iterativní proces. Začneme dole g 1 = 3 ↑↑↑↑ 3 a poté vytvoříme druhý řádek (řekněme to g 2) se šipkami g 1 mezi trojčaty.
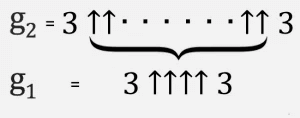
Pak g 3 jsou dvě trojice, oddělené g 2 šipkami nahoru, a tak dále, dokud g 64 s g 63 šipkami mezi trojicemi není Grahamovo číslo.
Pokud místo nesmrtelnosti zvolíte délku života rovnající se Grahamovu číslu, bude výsledek téměř stejný. I když předpokládáme, že podmínky ve vesmíru, ve sluneční soustavě a na Zemi navždy zůstanou nezměněny, lidský mozek by nevydržel tak dlouhou dobu bez škodlivých změn.

